Re: Explain Quantum Electrodynamics.

Dear Tania!

If you had asked this question without any reference to Feynman's book, I would just have advised you to read it --- but now, we're in some sort of trouble ;-). Maybe I can help to clarify some points by giving you a more concise account of Feynman diagrams.

Imagine two charged particles approaching each other. By means of their charge, they will `feel' each other's presence and repel or attract. Thus a `scattering process' takes place.
How is this accomplished? Well, in classical electrodynamics, we could calculate the outcome of such a process by solving a system of differential equations. The exact way the particles interact is built into those equations from the start --- we know that it's a Coulomb potential. Sounds simple, but the classical way is not the best way. For example, if an electron and a positron get scattered, there is a probability for them to not get just scattered but annihilate to give a pair of photons. This probability cannot be computed classically. So we need a better theory to explain such processes.
QED is this theory. The basic premise from which we start is that interactions like the ones described so far can be treated perturbatively, which means that one treats interactions as a small perturbation to a simpler, non-interacting `world'. Mathematically, it turns out that one can calculate scattering probabilities (s.a.) by summing up an infinite series of small corrections to the non-interacting case --- the case where the two particles don't scatter at all but just pass each other without notice. As one adds more terms to the series, one notices that they get smaller and smaller, so that the series finally converges to a finite value.
So far so good, but one may ask now what physical significance those many terms have. And that's where the Feynman diagrams come about: We can picture each term in the series as a scattering event between the two incoming particles, but they do not interact via a Coulomb field --- they exchange virtual particles (photons in this case).

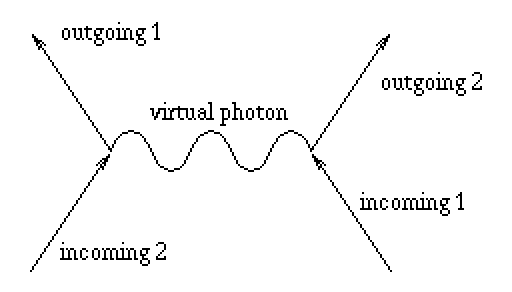
The simplest such process (the first one in the series) can be seen in the picture. A point where two electron (or positron) lines meet a photon line is called a `vertex' (the black dots in the picture). The more vertices a diagram contains, the more improbable the described event gets. This is because every vertex carries a small factor, and the probability of each event is porportional to the product of all factors at all vertices in the diagram. In QED, it turns out that this factor is nothing else but the electric charge.
So, Feynman diagrams are a way to picture terms in a perturbation series. As suggested by its mathematical structure, each term describes the exchange of a certain number of virtual particles. Now, to get the probability for a certain event with a certain accuracy, all one has to do is draw all allowed diagrams (i.e. allowed by the theory) with at most a certain number of vertices (i.e. one considers the perturbation series up to a certain point). Then there is a mathematical recipe to calculate numbers for each diagram, which in turn give the desired probability.

All right, I hope this has helped you to understand Feynman's book a little better. This reference might give you some more insight, or at least another point of view. If there's still much confusion left, don't hesitate to contact me by e-mail.

Happy Easter,
Georg.