Date: Tue Mar 16 14:19:04 1999
Posted By: Jason Goodman, Graduate Student, Massachusetts Institute of Technology
Area of science: Earth Sciences
ID: 921002010.Es
Message:
The analogy of a squirting garden hose isn't bad, but it isn't perfect
either.
I will begin my discussion by discussing a simpler problem, that of water
flowing along in a channel which encounters a bump in the bottom of the
channel. I'll then use ideas from this picture to discuss what happens in
the atmosphere. In everything that I'll describe, I'm assuming a
steady flow: that is, the velocity at every point is constant in
time.
Consider a smooth flow of water from left to right with velocity U through
a shallow channel whose depth is h. Let h vary with distance x along the
channel -- specifically, let the depth be uniform everywhere except for a
hill at x=0. What happens when the water goes over the bump? I won't show
you the mathematics, but there are two possibilities:
- The layer of water gets thicker as it passes over the bump. If this
happens, the speed of the water above the bump must be slower than
elsewhere to allow the same number of liters per second to flow over the
bump as everywhere else. (If this were not true, water would keep piling
up behind the bump!) But if the water is going to decelerate as it goes
over the bump, there must be a force to push it. This force is the
pressure, which is low upstream from the bump and high on top of it.If
the pressure in the water above the bump is high, there must be more weight
of water pressing down on it -- therefore, the water surface must be
slightly higher there. You can also think of this as water going from low
altitude to high altitude, gaining potential energy and losing kinetic
energy as it does so.
- The layer of water gets thinner as it passes over the bump. If this
happens, the water must speed up to allow constant mass transport over the
bump. To speed up, there must be low pressure on top of the bump, and
thus a depressed water surface.
Both of these possibilities have consistent physics: which one occurs in
practice depends on U/sqrt(g H), where g is the acceleration of gravity, H
is the depth of the fluid, and U is the mean flow speed. Note that sqrt(g
H) is the speed of waves on the surface of this fluid. If the flow speed
is less than the wave speed, U/sqrt(g H) < 1, and we get the first case
above, which is called "subcritical" flow. If the flow speed is more than
the wave speed, U/sqrt(g H) > 1, and we get the second case, called
"supercritical" flow. These cases are illustrated below.
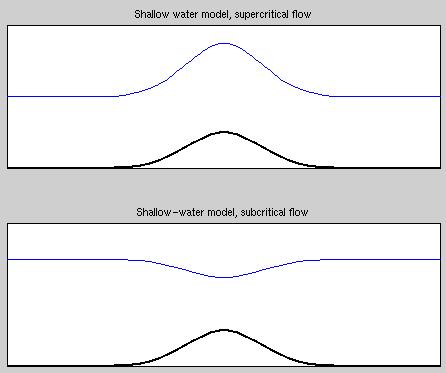
The key difference between the two cases is that for subcritical flow, a
surface wave can travel forward ahead of the bump to "warn" the water that
the bump is coming. But for supercritical flow, the wave can't go upstream
faster than it's carried downstream by the current, so the water hits the
bump without "warning" and piles up there.
Putting your thumb over a garden hose is a good example of a subcritical
flow: the pressure in the hose is higher than the pressure right where your
thumb is, so the water accelerates through the constriction and out of the
hose. The ratio of wave speed to flow speed is still important, although
this time, the waves in question are sound waves travelling
through the water in the hose. Supercritical flows in this case are
supersonic. An airplane travelling at supersonic speed through
the air piles up air in front of it just as the bump piles up water in the
figure above.
The parallel between supersonic air flows and supercritical flows over
bumps in a channel goes even farther. Have you ever watched water flow
over a rock in a stream, and seen it form a foaming, turbulent wave that
hangs behind the rock? That's a sudden transition between supercritical and
subcritical flow, which is similar to the sudden transition between
supersonic and subsonic flow which occurs in the shock wave of a supersonic
airplane!
Anyway, on to the second example, which should answer your question. Now
we consider flows of air over mountains. While the atmosphere doesn't have
an upper surface like a water-filled channel does, it does have layers of
heavier and lighter air. If you took air from high in the atmosphere down
to ground level in a rubber balloon, you would find it was much lighter
than the ground-level air. It acts a lot like a mixture of oil and water:
if you play with a bottle of oil-and-vinegar salad dressing, you can make
waves which slosh around on the interface between the two fluids. These
are much like water waves, but move more slowly. The atmosphere has
similar "internal waves", but the tricky bit is that there are
lots of layers (we call it a "continuously stratified fluid").
So, since the atmosphere has "internal waves" which act a lot like water
waves, we might expect the behavior to change greatly depending on whether
the wind speed is subcritical or supercritical with respect to the internal
waves. And, indeed, it does. My second figure shows a sketch of the
mathematical result for a series of sinusoidal hills on the ground (which
is the simplest case to handle.)
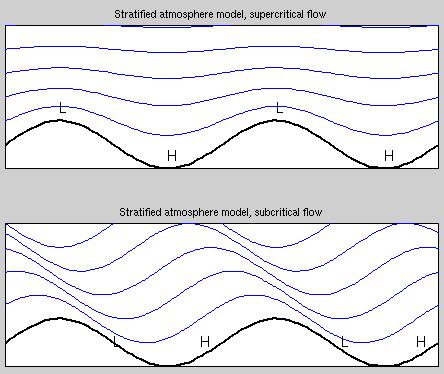
The blue lines are "streamlines", which show the path of individual
particles within the fluid. When streamlines are closer together, the flow
speed is higher. The letters "H" and "L" correspond to high and low
atmospheric pressure. In the top panel, we see what happens when the wind
speed is very high. We get low pressure and accelerated flow over the tops
of the hills. In this case, the atmosphere's response to the hill's
presence dies out as we go up. As a result, flow speed must be higher over
the hils, and so there must be low pressure at the hillcrests to accelerate
the winds. The bottom panel shows what happens when the wind is slower --
the flow is subcritical. Internal waves are able to propagate upstream and
vertically upwards, carrying the pressure signal forward -- you can see
them in the figure. Now, wind speeds are largest (streamlines are closest
together) down the backside of the hills, and the air pressure is lowest
there.
Whether you get supercritical or subcritical flow in this situation depends
on the value of (2 pi U/NL), where U is the wind speed, L is the
wavelength of the hill, and N is a measure of how rapidly the air changes
density with height. If this value is greater than one, the flow is
supercritical; if it is less than one, the flow is subcritical. A typical value of N is 0.01 1/seconds. So if the
wind speed is 10 meters per second, flow over a hill 1 kilometer across
would be supercritical (and thus look like the upper panel) while flow over
a mountain 10 kilometers across would be subcritical (and thus look like
the lower panel).
So you see that the pinched-hose analogy is both helpful and misleading.
In all cases, the pressure is lowest where the velocity is highest. In the
pinched hose and in the supercritical atmospheric flow, the flow
accelerates because it must pass the same volume per unit time through a
smaller aperture, but the pinched hose is subcritical, unlike the
atmospheric case it resembles. In the garden hose, the flow has low
pressure at the location of maximum constriction, while in the atmosphere
the maximum velocity for subcritical flows (which are very common) is found
behind the hills rather than on top of them, and the pressure is
lowest behind the hills.
Current Queue |
Current Queue for Earth Sciences |
Earth Sciences archives
Try the links in the MadSci Library for more information on Earth Sciences.
MadSci Home | Information |
Search |
Random Knowledge Generator |
MadSci Archives |
Mad Library | MAD Labs |
MAD FAQs |
Ask a ? |
Join Us! |
Help Support MadSci
MadSci Network,
webadmin@www.madsci.org
© 1995-1999. All rights reserved.

