Date: Wed Jul 28 12:06:33 1999
Posted By: Demian Bertozzi, Grad student, Physics, UFSC
Area of science: Physics
ID: 934812662.Ph
Message:
Hey, Joe! The way I see, It's a pure geometrical question, not Physics.
Look at the picture.
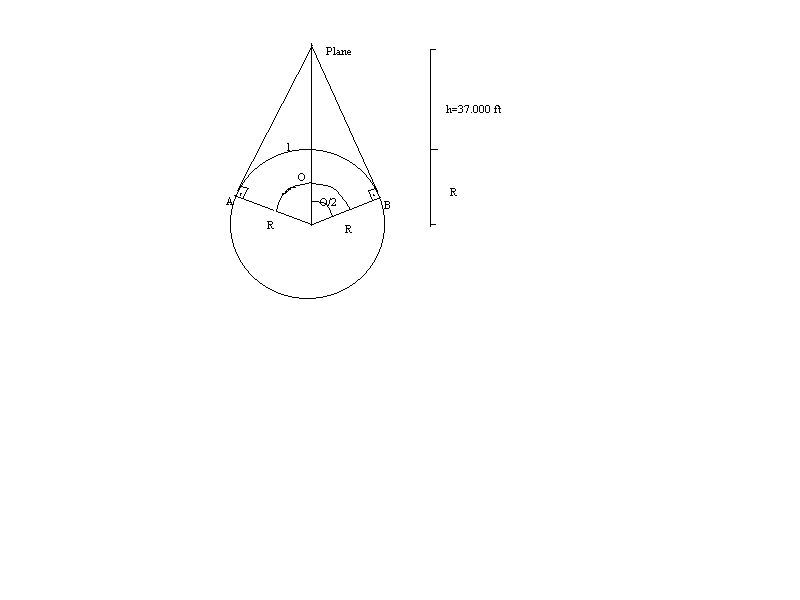 We want to know the length of the arc AB. We only need to know the angle
which determines the arc, so l = .R , where R is the Earth radius. R
is aproximatelly equal to 6.400 km, but I don't know this value on ft ,
so itís an exercise to you. The angle is easy to determine. Note that cos
(/2) = R/(R+h). The angle is exactly /2 because the two triangles are
equivalent. With a calculator, you can imediatelly obtain . However, you
can use this relation
Cos (/2) = ( (1+ cos ) / 2 )Ĺ
to take directly the cos .
You may want to know that I did a rough aproximation on solving
this question. I put the plane to travel right above the equator line,
following its direction, because at that point the section (cut) of the
Earth is a circle with R=6.400 km. If the plane, for instance, were
travelling perpendicularly to equator, the section would be na elipsis,
but I think my way is a reasonable aproach for what you need.
Hope this helps.
D..!
Any doubts to escrutinador@hotmail.com
We want to know the length of the arc AB. We only need to know the angle
which determines the arc, so l = .R , where R is the Earth radius. R
is aproximatelly equal to 6.400 km, but I don't know this value on ft ,
so itís an exercise to you. The angle is easy to determine. Note that cos
(/2) = R/(R+h). The angle is exactly /2 because the two triangles are
equivalent. With a calculator, you can imediatelly obtain . However, you
can use this relation
Cos (/2) = ( (1+ cos ) / 2 )Ĺ
to take directly the cos .
You may want to know that I did a rough aproximation on solving
this question. I put the plane to travel right above the equator line,
following its direction, because at that point the section (cut) of the
Earth is a circle with R=6.400 km. If the plane, for instance, were
travelling perpendicularly to equator, the section would be na elipsis,
but I think my way is a reasonable aproach for what you need.
Hope this helps.
D..!
Any doubts to escrutinador@hotmail.com
Current Queue |
Current Queue for Physics |
Physics archives
Try the links in the MadSci Library for more information on Physics.
MadSci Home | Information |
Search |
Random Knowledge Generator |
MadSci Archives |
Mad Library | MAD Labs |
MAD FAQs |
Ask a ? |
Join Us! |
Help Support MadSci
MadSci Network,
webadmin@www.madsci.org
© 1995-1999. All rights reserved.
 We want to know the length of the arc AB. We only need to know the angle
which determines the arc, so l = .R , where R is the Earth radius. R
is aproximatelly equal to 6.400 km, but I don't know this value on ft ,
so itís an exercise to you. The angle is easy to determine. Note that cos
(/2) = R/(R+h). The angle is exactly /2 because the two triangles are
equivalent. With a calculator, you can imediatelly obtain . However, you
can use this relation
Cos (/2) = ( (1+ cos ) / 2 )Ĺ
to take directly the cos .
You may want to know that I did a rough aproximation on solving
this question. I put the plane to travel right above the equator line,
following its direction, because at that point the section (cut) of the
Earth is a circle with R=6.400 km. If the plane, for instance, were
travelling perpendicularly to equator, the section would be na elipsis,
but I think my way is a reasonable aproach for what you need.
Hope this helps.
D..!
Any doubts to escrutinador@hotmail.com
We want to know the length of the arc AB. We only need to know the angle
which determines the arc, so l = .R , where R is the Earth radius. R
is aproximatelly equal to 6.400 km, but I don't know this value on ft ,
so itís an exercise to you. The angle is easy to determine. Note that cos
(/2) = R/(R+h). The angle is exactly /2 because the two triangles are
equivalent. With a calculator, you can imediatelly obtain . However, you
can use this relation
Cos (/2) = ( (1+ cos ) / 2 )Ĺ
to take directly the cos .
You may want to know that I did a rough aproximation on solving
this question. I put the plane to travel right above the equator line,
following its direction, because at that point the section (cut) of the
Earth is a circle with R=6.400 km. If the plane, for instance, were
travelling perpendicularly to equator, the section would be na elipsis,
but I think my way is a reasonable aproach for what you need.
Hope this helps.
D..!
Any doubts to escrutinador@hotmail.com