Re: Please give me DETAILED derivation of gravity inside a sphere

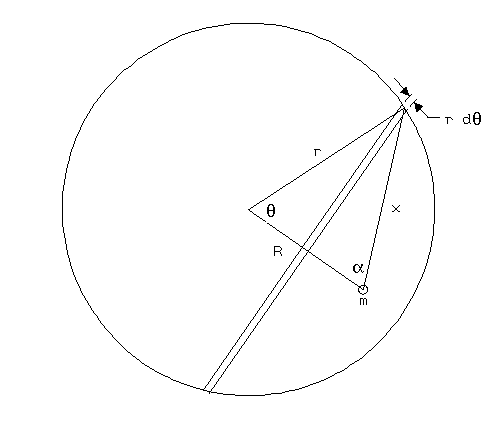
I will follow the derivation that I learned in college freshman physics from Halliday and Resnick ("Physics", David Halliday and Robert Resnick. John Wiley and Sons publishers. I have the old first edition from 1966!). In my old 1966 version of the book the derivation starts on page 397 and is section 16.6: "Gravitational Effect of a Spherical Distribution of Mass". Here's a sketch to help us:

This is going to involve a lot of equations, so hang on to your desk!!! This derivation depends on calculus, so if you haven't studied that yet you may have to wait until you know calculus to fully follow the derivation. You can depend on the results of the derivatives and integrations, however, as all the equations have been reviewed for accuracy.

We start by considering a uniformly dense thin spherical shell of radius r. Each particle or small chunk of the shell will exert a gravitational force on our test mass m (the one we want to know how it will behave near our spherical shell) which is proportional to the mass of the small chunk and inversely proportional to the square of the distance between it and our test mass, and directed along the line joining them. That is,
df = Gm dM/x²
where df is the gravitational force due to the interaction between m and dM, G is the universal gravitational constant, m is our test mass, dM is the mass of the small chunk of the shell, and x is the distance separating the centers of mass. Our task is to sum up the contribution of all the chunks of mass comprising the shell. We are helped out by symmetry, as follows.

Let's put our test mass inside the shell but off center, and consider a thin ring of the shell which is centered around a line joining the center of our test mass and the center of the thin shell, the line being labeled R. In the sketch we have depicted the thin ring as just a slice of a circle, but imagine it as a full ring of material around the sphere. Each small particle or chunk of the thin ring of material will have, directly opposite it symmetrically opposed across this joining line, another particle or chunk just like it. In the dimension that joins the two opposed chunks, the force of gravity on our test mass cancel out. This is true for every particle or chunk of the entire shell of material, so the only dimension that we need to consider for the net force on the test mass is along the line joining the centers, or parallel to the line R!!! It should be obvious that this is a very fortunate simplification in our problem. (It turns out that the full three-dimensional treatment is not too complicated, though.)

Okay, so now we know we only have to sum up the gravitational contribution in a direction parallel to the line R. Let's figure out the mass dM of a portion of the ring of material. It has a radius of
r sin q, its width is
r dq and its thickness we shall call t. There is another angle that I have not shown on the sketch, which is the rotation angle around the line R, which I shall call f. So the length of dM is
r sin q df. So the volume dV of the little piece of the ring is
dV = t r dq r sin q df
dV = tr² sin q dq df.
If we call the density r the mass dM is then
dM = r dV = t rr² sin q dq df.

The effective force exerted by dM on the test mass m is directed along the line R, as we discussed at the start, and so has the magnitude dF where
dF = df cos a
dF = (cos a ) G m dM / x²
and substituting the above expression for dM we get
dF = (cos a ) G t r m r² sin q dq d f / x²
We can integrate dF around the angle f, which gives us (since the integration limits are zero to 2 p) a multiplier of 2p. So the force dF resulting from the entire ring of material is then
(equation 1) dF = (cos a ) 2p G t r m r² sin q dq / x²

Fortunately the variables x, a, and q are related. You can work out from the sketch that
(equation 2) cos a = ( R - r cos q ) / x
and by the law of cosines
x² = R² + r² - 2Rr cos q
so we have
(equation 3) r cos q = ( R² + r ² - x² ) / 2R

Now, we need some relations between the various infinitesimal parts. We start this by differentiating the equation
x² = R² + r² - 2Rr cos q
(which is from the law of cosines) to obtain
2x dx = 2Rr sin q d q
or
(equation 4) sin q d q = x dx / Rr

Substituting eqn 3 into eqn 2, and then eqn 2 and eqn 4 into eqn 1, we have eliminated q and a to obtain
(equation 5) dF = ( pGt rmr / R² ) ( (( R² - r ² ) / x²) + 1 ) dx
which is the force exerted by the circular strip on the test mass m.

Finally, we sum up the contribution of all the circular strips that comprise the spherical shell. This is an integration over the spherical shell with respect to the variable x, and we know that x ranges from a minimum of r - R to a maximum of r + R. So the integration is with equation 5 using these limits on x. The integral of
(( R² - r² ) / x²) + 1 with respect to x is
(( r² - R² ) / x ) + x
which, when evaluated between the limits r - R and r + R is exactly equal to zero!!!!. This means that inside a uniform density spherical shell the net gravitational attraction to the small test mass m is exactly zero, and is independent of the mass's position inside the shell!! It's amazing, but true.

John Link, MadSci Physicist