Re: How far can you see before the curviture of the earth falls out of site?

To answer this question I had to dig up some geometry and algebra.  It 
sounds like an easy question, but before long you have to use triangeles in 
circles, so I will have you set up a demonstration, and show you a picture.  

Since the answer depends on how far off the the earth your eyes are, I will 
first give you the answer as if you were standing on a 1,000 foot tower, and 
then if you are four feet tall.  If you can work out how to do the math on 
your own (which I hope you try to do... or get someone to help you) then you 
can figure this question out for any height.

The demonstration:  Get an army man or some other action figure and stand 
the figure on a ball.  You will see that the smooth surface of the ball is 
falling away from the action figure in all directions.  That is what is 
happening to you as you stand in the middle of your “flat” field.   Take a 
string and draw it from the figure’s eyes to where it skims the surface of 
the the ball (in math terms: becomes tangent to the sphere).  This string is 
how far you see.  To figure out this length - this is where the geometry and 
algebra come in.  (I know you could measure the string with a ruler.... but 
out in the field, unless you have a very good friend, and lots of string, 
you just can’t use a ruler out there).  So onto the MATH.  Make a triangle:  
Start from the figures' eyes and make an imaginary line from the eyes to the 
very center of the ball (Line Q).  From the very center of the ball, make 
another line to the point where the string touches the ball - is tangent to 
the ball (line R).  The third line is the string (line S). 


 

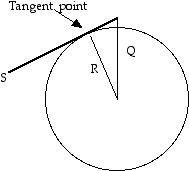The reason I had to involve the center of the ball is because I wanted to 
make the triangle a right triangle (one with a "right" or 90 degree angle)
That means we can use the pythagorian theorom: a^2 + b^2 = c^2
In english this means (side a x side a) + (side b x side b) = 
(side c x side c).
  
	When you use this formula on a right triangle, the longest side, or 
hypotenuse must always be side c, so for us this is line Q.  We also know 
another side, line R, and we can make this line a 

We know side R because that is the radius of the earth (3947 miles or 
approximately 20,840,000 feet)

We know side Q because that is the radius of the earth + the height of the 
lookers eyes - and for this problem we will put our watcher on a 1,000 foot 
tower (so Q = approximately 20,841,000 feet)

so a^2 = 20,840,000 ^2 = 434,305,600,000,000
and c^2 = 20,841,000 ^2 = 434,347,281,000,000

So we rearrange the original formula so we can solve for b (line S, the 
string) to get

b^2 = c^2 - a^2 or

b^2 = 434,347,281,000,000 - 434,305,600,000,000 = 41,681,000,000

next take the square root of 41,681,000,000 (which is b^2)
so b = 204,159 ft or about 40 miles!

Now if our person is standing on the ground and is about 4 feet hight, you 
can probobly guess that the distance the person would see is going to be 
much less than 40 miles....  

in fact our 4 foot person will see about 2.4 miles

I'll show the work below

a (line R) = 20,840,000 feet
c (line Q) = 20,840,004 feet

so b^2 = 20,840,004 ^2  - 20,840,000 ^2 = 166720000 

and b = 12912 feet or 2.44 miles

GOOD LUCK!

and many thanks for the challange
Greta Hardin

P.S.  A few things to be aware of in problems like this!
First notice that I kept using numbers with lots and lots of digits until 
the very end of the problem.  That's because when you are doing a math 
problem you need to realize that all the digits are important.  These are 
called "significant figures."  In other words don't throw away too many 
numbers until you get to the end of the problem.  If you are interested in 
what significant figures are, you can look them up... and this will serve 
you well as you go on in math and science!   


P.P.S.  This problem can also be used using trigonometry.  I'll show you the 
1000 foot tower version that way.  

Now -to be able to find out anything about a tringle - and here we want to 
know the distance of S from the eyes to the tangent point - you need to know 
at least 3 things about the triangle.... and we do - we know 2 sides and one 
angle!

We know side R because that is the radius of the earth ( 3947 miles or 
approximately 20,840,000 feet)

We know side Q because that is the radius of the earth + the height of the 
lookers eyes - and for this problem we will put our watcher on a 1,000 foot 
tower (so Q = approximately 20,841,000)

And we know the angle between sides S and R is 90 degrees because we made it 
that way on purpose.
To find the length of side S we need to find out one more angle:
The angle between sides S and Q  will work nicely.

To find angle SQ we first find its sine

sin SQ = opposite side / hypotenuse = R/Q =  20,840,000/20,841,000 = 0.9995

now find the inverse of the sine and we get the angle 89.44 degrees

now to get side S we can use the cosine of the angle SQ

cos SQ = adjascent side/hypotenuse = S/Q

cos 89.44 = S/20,841,000    --->  cos 89.44 x 20,841,000  = S

S = 0.009796 x 20,841,000 = 204,159 feet  or about 40 miles.

See it works both ways!