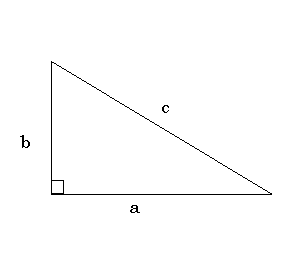
| MadSci Network: Other |
Admin note: The follwing is true only if you assume that both dimensions of the rectangle are equal. Please see the bottom of this page for further details.
-------------
Hi Tom,
Your answer lies with the Pythagorean Theorem:\
"In a right-angled triangle, the area of the square on the hypothenuse (the longest side) is equal to the sum of the areas of the squares drawn on the other two sides."
There's a nice interactive program to prove this at the following site:
http://www.geocities.com/CapeCanaveral/Launchpad/3740/diagram.html
The mathematical formula is a^2 + b^2 = c^2 , where a and b are the sides that form the right angle and c is the side opposite the right angle.
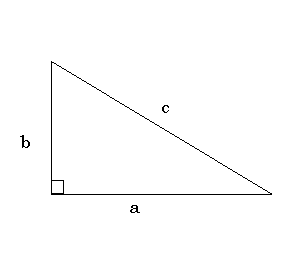
Since a T.V. is a rectangle shape, you can break it down into two right- angled triangles by cutting the rectangle across diagonally. In your case, the diagonal is 13". As the diagonal is also the longest side in the triangle, c = 13, so c^2 = 13^2 = 169.
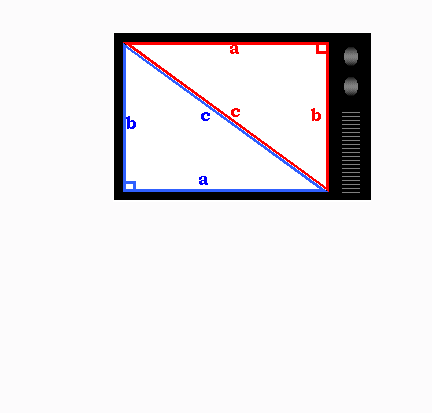
Now that you know what one side of the equation is, you need to figure out the other side. a^2 + b^2 = 169. In the case of a t.v., one side; a, is going to be the width of the screen, and the other side; b, will be the height of the screen.
In order to find the area of a rectangle, you multiply the width by the height, as in a x b.
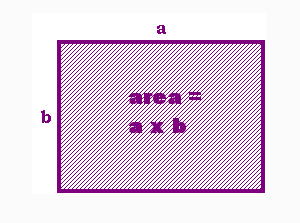
Since you do not know what the ratio of the width of the screen is relative to the height of the screen, and in order to simplify the math, assume that width and height are the same; a = b (this will not affect the area because one of the three sides is constant)
Then your Pythagorean Theorem would be; a^2 + a^2 = 169
And now the fun begins!
Add like terms
=> 2a^2 = 169Divide by 2
=> a^2 = 84.5Take the squareroot of both sides
=> a = 9.2 inches = bYou now have values for both your height and width so you can use the formula to find the area of a rectangle.
To find area, a x b => 9.2" x 9.2" = 84.4 squared inches

This value is not going to be exact since the screen of a tv is not completely square, but you would need to use calculus to determine the precise area, and only for a few squared inches.
Thanks for your question!
Evelyne
-------------
Admin note continued:
James Griepenburg adds the following:
The area of a rectangle of constant diagonal decreases as the rectangle flattens from a square approaching 0 as the other angles approach 90 and 0 degrees.
The area of a rectangle of fixed diagonal length (d) can be calculated from
area = d^2 x cos(theta) x sin(theta),
where theta is the angle of the diagonal from the horizontal.
-----------
We also received the following comment:
No - given just the length of the diagonal, you cannot calculate the area of a square. Specifying the length of the hypotenuse of a right- angle triangle does not determine its area. This can be proved by trying two or three random lengths for side 'a'. Calculate side 'b' (Pythagoras), and then determine the area from those sides. It can be shown experimentally by drawing a right angle on graph paper (as 'axes'), and placing a straight edge (any kength will do)with each end touching an 'axis' (you can draw the straight line if you want). Count the squares. Repeat with lines at other angles. Note the area is a maximum at 45 degrees (when the other two sides are equal).
Try the links in the MadSci Library for more information on Other.