Re: Fermat's principle in optics

Fermat's principle (which many people regard as really neat!) says that the path of a light beam between two points always follows the route that takes the least time to traverse. Surprisingly, this principle encapsulates the laws of reflection and refraction, and might be considered as more fundamental.

Anyway, I think what you are really asking is whether Fermat's principle can be used to derive the shape of a mirror which will focus parallel rays to a single focal point. The answer is yes, but it requires a diagram to see why!

Consider a mirror placed flat, looking up at the sky. Light rays from a distant object (the distance is d) directly above the mirror (whose shape we don't know yet) hit it, and are brought to a focus at point C.

A ray of light which hits the centre of the mirror O bounces straight back, and traverses a total distance d+f from the source to the focal point, where f is the focal length.

Another ray of light, parallel to the first, hits the mirror at a point which is offset from the centre by a distance x horizontally and y vertically. It then travels a further distance r, to reach the focal point, so the total distance it travels from the source is d-y+r.

Now, Fermat tells us that for the rays to follow both paths from the source to arrive at C, the path lengths must be the same. Hence:

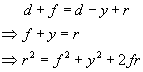
But from Pythagoras we also know:

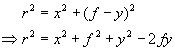
So, finally we find:

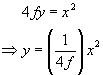
Which tells us that the shape of the mirror must be parabolic (as expected), with the steepness depending on the focal length (again as expected)