Re: Longitude versus altitude which is closer to the sun?

Dear Leslie, 

thank you very much for your question, which i must admit needs a lot of 
discussion. I will give you first some basic information regarding earth 
and its relation to the sun.

1)Earth's distance from the sun is approximately:

  152100000km at Aphelion and
  147090000km at Perihelion.

As you can see these numbers are quite large, which means that a 
difference of 4365meters is neglectible.

2)Earth is rotating around its axis. This is why we have day and night. 
Now this is very crucial to your question regarding the longitude 
coordinates (East-West).

3)Earth is rotating around the sun but its axis is tilted by 23.5degrees 
and this is why we have the various seasons.

Now lets examine the coordinates you provided. These coordinates are 
called geographic or geodetic coordinates and of course are part of a 
coordinate reference system which is defined by the Greenwich
meridian and the equatorial plane. If we look this reference system from
space we'll see that it is fixed only for us on earth. This is due to the fact
that the earth is rotating around its axis. So when for e.g. you say 97 degrees 
West X degrees North this would not be a fixed spot for someone who is looking
down on earth from a spaceship, since he would watch it move below him. So if
two points had the same latitude but different longitude we would have to
specify also the time at which we would want to calculate their distance from
the sun.

So in order to answer your question i will have to make certain 
assumptions:
1)The earth is not rotating
2)I will ignore the longitude (as explained in the previous paragraph) and 
assume that both points are in the same longitude
3)I will consider earth to be a sphere with a mean radius R=6371Km
4)I will assume that the earth's position towards the sun is the one 
during December
5)The earth and the sun lay on the same plane defined by an horizontal 
line passing from the earth's and the sun's center as shown in the figure.

This means that we will now give an very approximate value for the 
distance between point A (42.87N and 4365meters height) and point B 
(34.52N and 0 meters height). I will explain the calculation for point A 
and point B can be calculated in the same way.

-According to the figure (a simple figure just for understanding what i am 
going to do) we know the geographic latitude and we have to calculate 
first the geocentric latitude which is defined by (AES). Since we assumed 
that the earth is a circle and not an ellipsoid of revolution (as 
geodesists do for more precise calculations) then the geographic latitude 
is equal to the geocentric latitude.




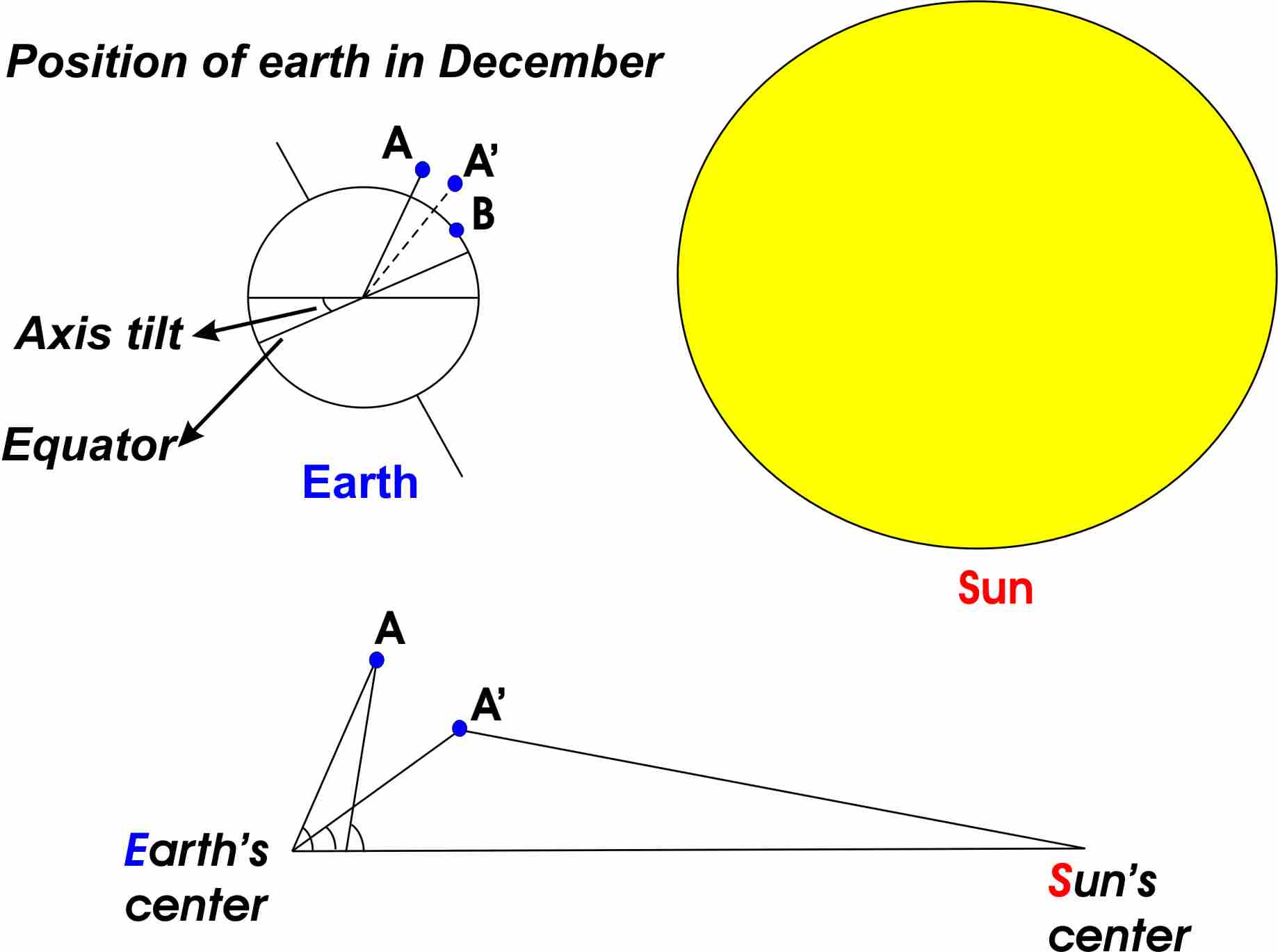-Now we will add the tilt of the earth's axis. This is done by adding 23.5 
degrees to 42.87N which will give us:
42.87 + 23.5 = 66.37 degrees and this is point A in the figure
If there weren't any tilt then point A' would be the one that we would use

-We calculate the distance of point A from the earth's center which is 
height + mean Radius of the Earth:
6371000meters + 4365meters = 6375365meters or 6375.365km

-Now our problem is to find the distance (AS) which is what we are looking 
for. The (ASE) form a triangle where we know the distances (A'E),(ES) and 
the angle (AES). The solution is given by the following expression:
(AS) = square root of( AE^2 + ES^2 - 2*A'E*ES*cos(AES) )
which gives: (A'S)= 6375.365^2 + 152100000^2 - 2 * 6375.365 * 152100000 * 
cos(66.37) =>
(AS) = 152097444km

For (B'S) following the above procedure we'll have:
(BS) = 6371^2 + 152100000^2 - 2 * 6371 * 152100000 * cos(58,02) =>
(BS) = 152096625km

By comparing both results we see that point B is closer to the sun then 
point A. We must not forget that we reached to this result after making 
certain assumptions, which of course leads us to make calculations under 
an ideal enviroment.

I will gladly answer any further questions or comments, thanks again for 
thinking as a mad scientist:)

Vassilios N. Grigoriadis
MSc Surveyor Engineer
Thessaloniki, Makedonia
Greece (Hellas)

{Admin note: Although Vassilios made a number of assumptions and simplifications in his 
calculation, the bottom line is quite clear: If we are thinking about how close to the sun we are, 
latitude is much more important than altitude as a determining factor. }