Re: which falls faster? A tennis ball or golf ball?

First, there is some really good information in our archives dealing with the falling of objects in the atmosphere, which you can find by using our search engine to search on "terminal velocity". Among the answers that are listed are these:

an answer I wrote

another answer I wrote

I also did a Google search on "terminal velocity" and found these good web pages:

includes a Java calculator

at hyperphysics (This page gives the terminal velocity of a golf ball as 32 m/s.)

aerodynamics of different balls

another calculator

I also searched for information about tennis balls: (The previous answers have all the information about golf balls.)

tennis ball 1

tennis ball 2

the fuzz changes with speed

Okay, so let's apply some of this information to your question. The pertinent data on the two types of ball are:

golf ball:
mass: 46 g
diameter: 42.7mm
(resulting density: about 1.13 g/cm³)

tennis ball:
mass: 57 g
diameter: 65mm
(resulting density: about 0.40 g/cm³)

One of the most interesting things about the acoustoscan site is that the generally accepted coefficient of drag for a spherical object does not exactly fit for either a golf ball or a tennis ball! For the golf ball at low velocities C_d is closer to 0.45 , and for a tennis ball at low speeds we should use C_d = 0.6.

To discuss some of the details prior to the balls' obtaining terminal velocity, one of the previous answers contains a spreadsheet that was used to simulate the fall of a golf ball. That spreadsheet can also be used to simulate the tennis ball simply by changing some of the data at the top of the spreadsheet. For the golf ball change C_d from 0.5 to 0.45. Make a separate copy of the spreadsheet and use the following data for the tennis ball:
C_d = 0.6
area = 0.0033 m²
mass = 0.057 kg
(Having two copies of the spreadsheet allows you to have both sets of data open at the same time on the screen, for easy comparison.)

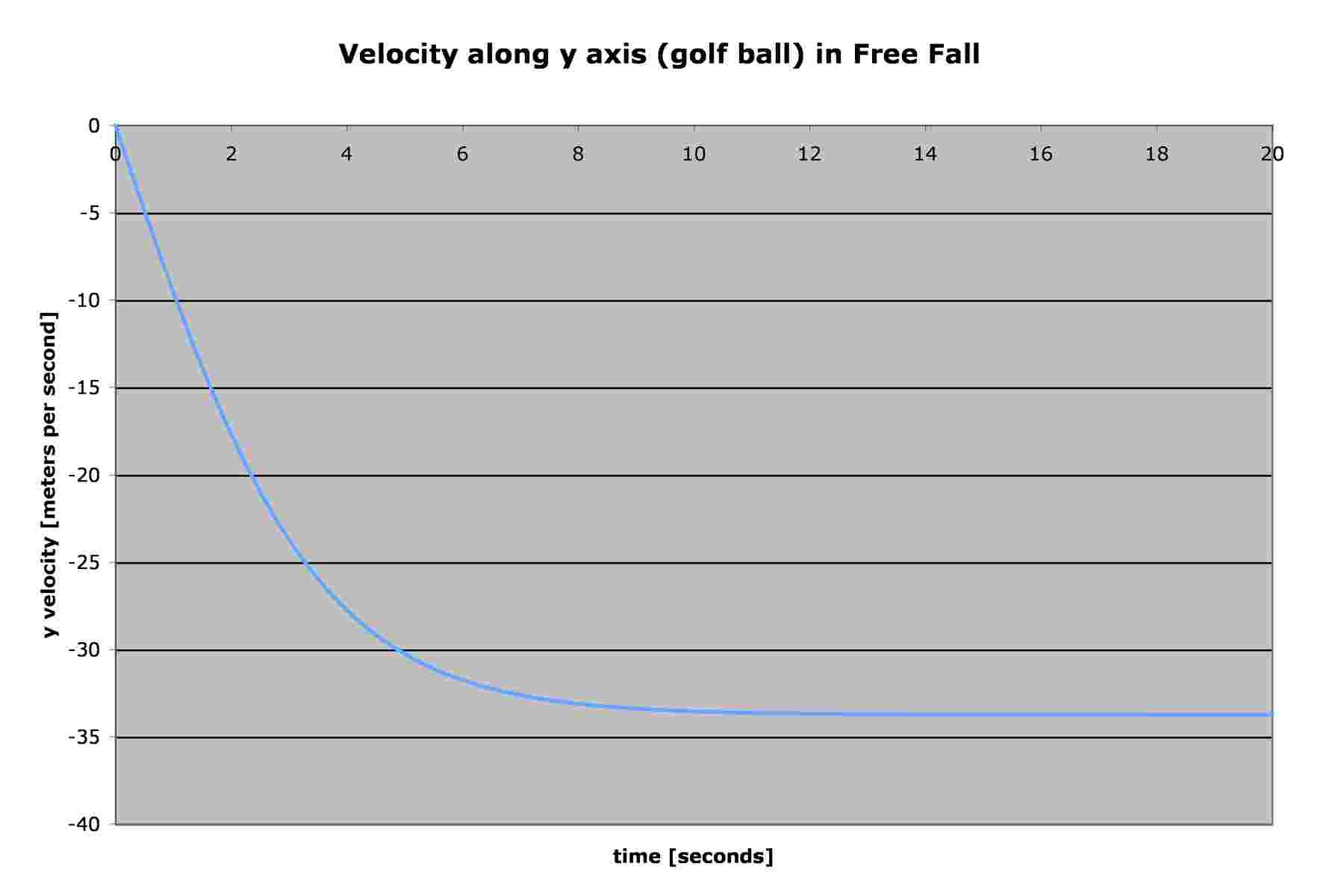
Some readers may not have easy access to Excel, so here are the graphs that are obtained:

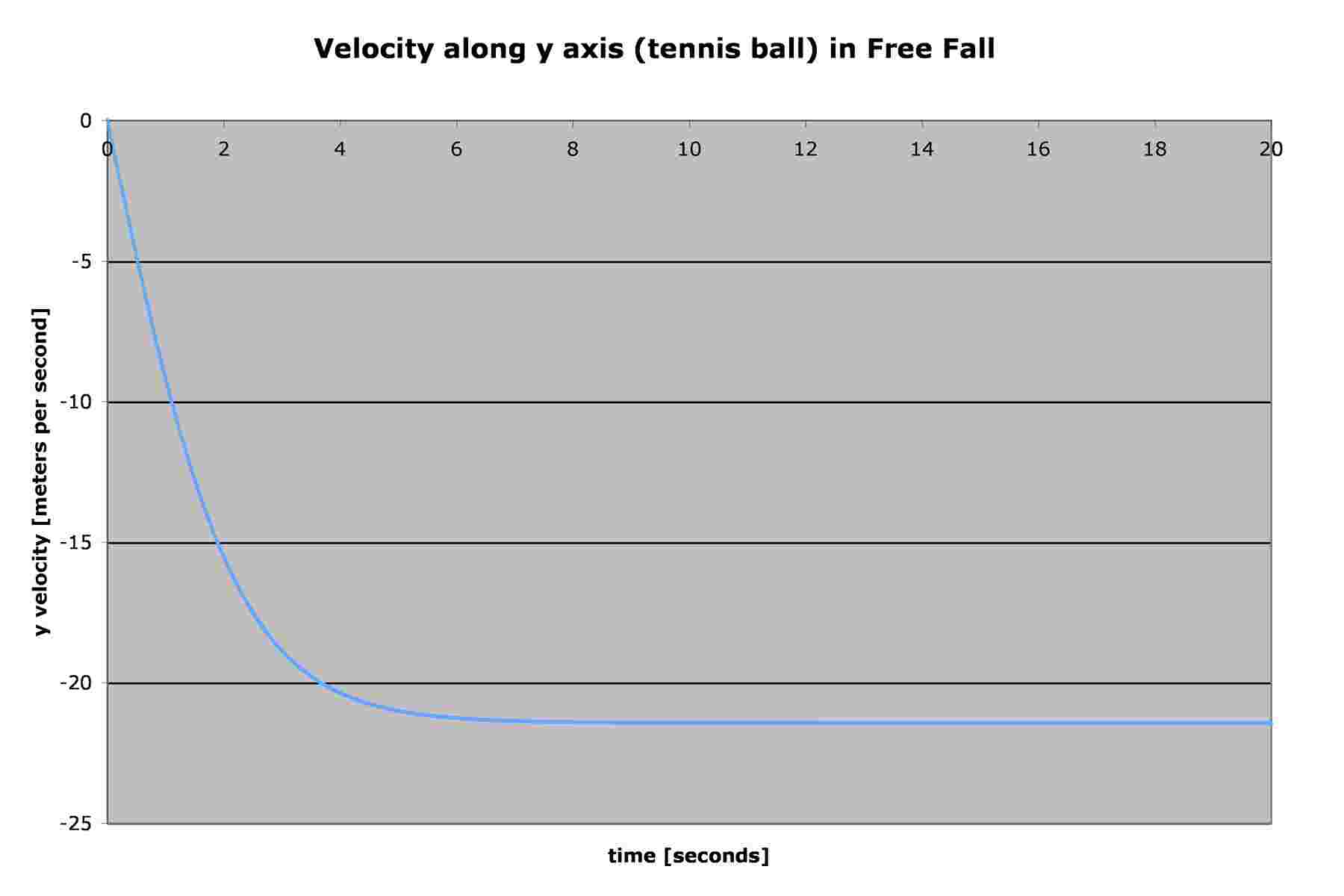
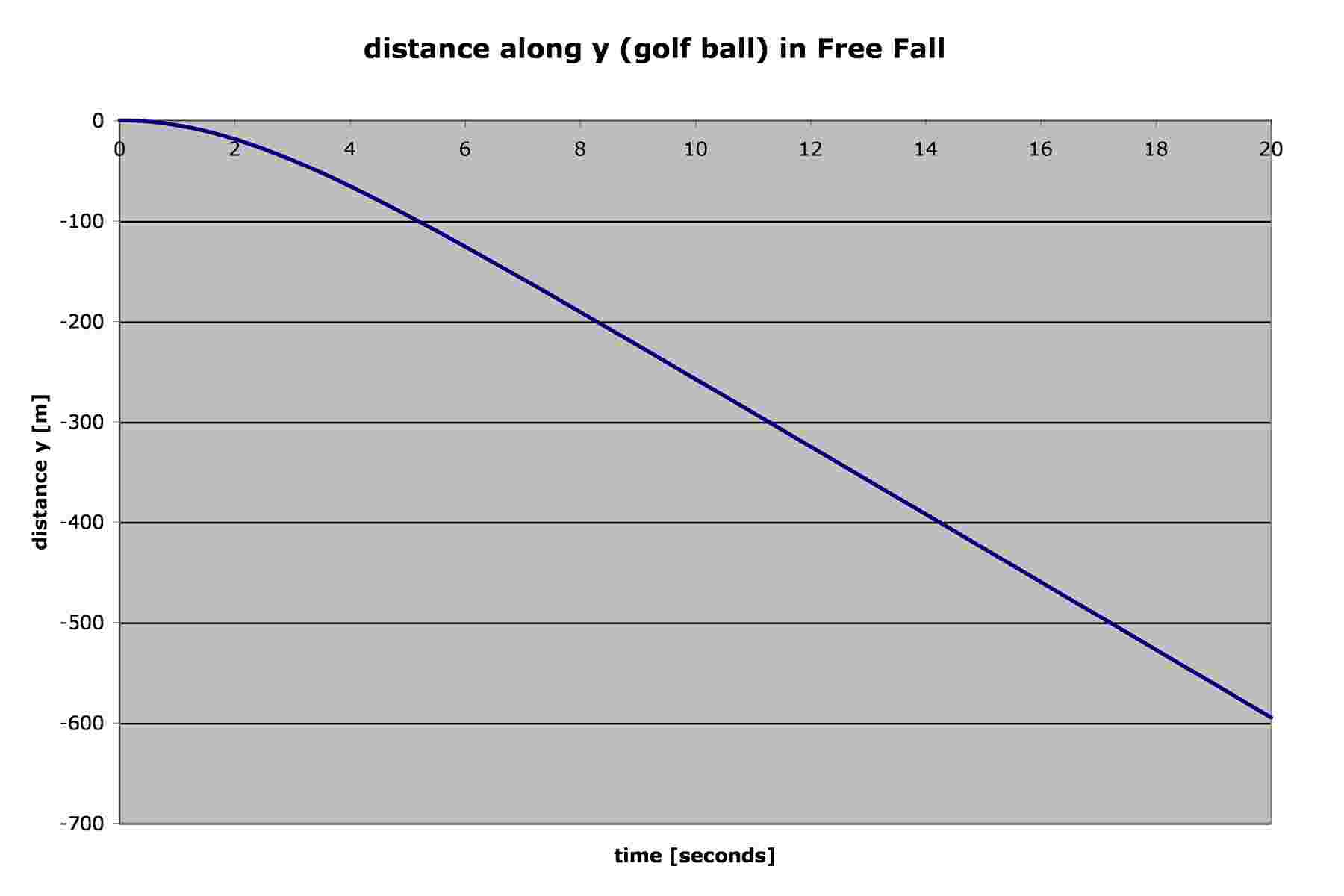
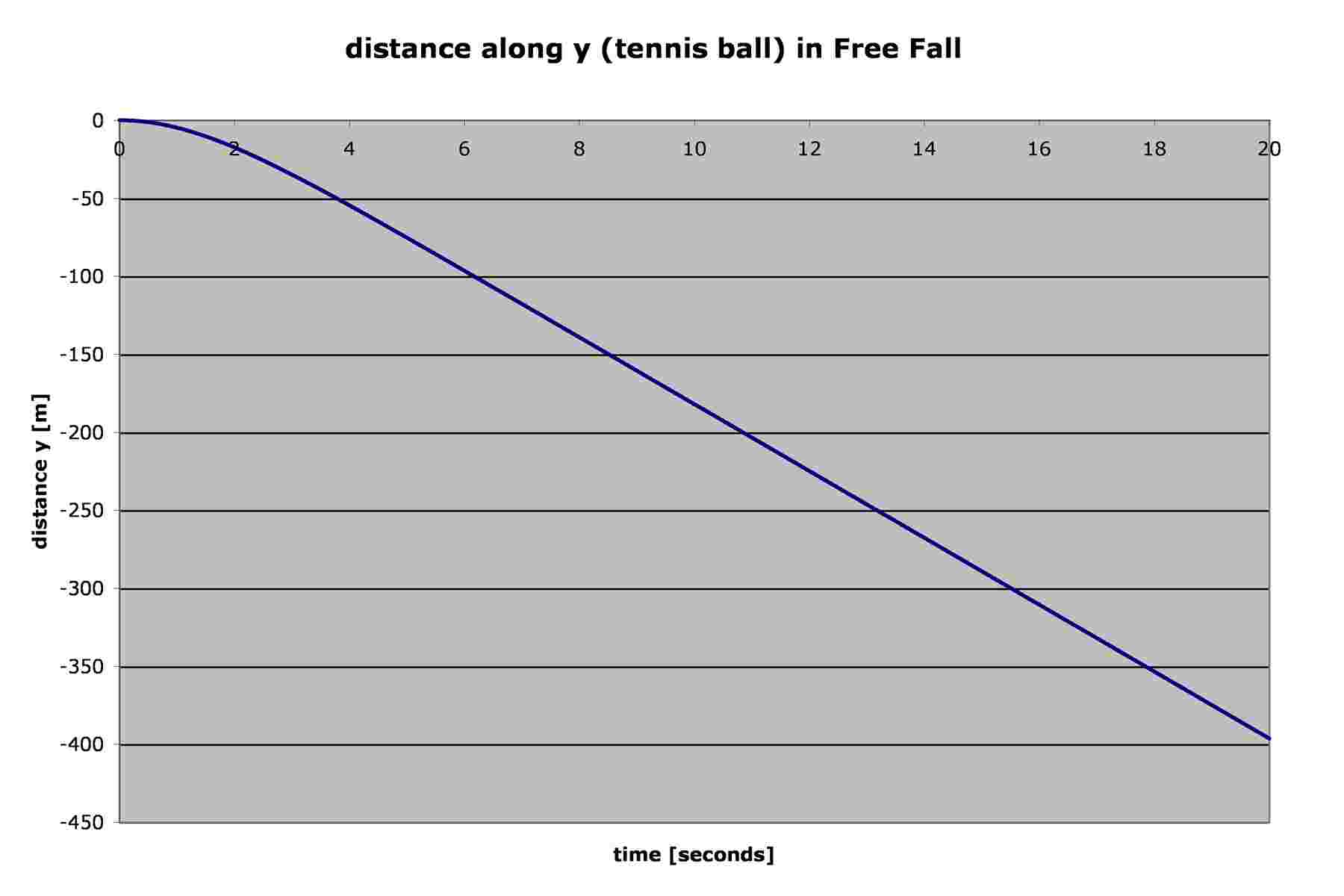
If you do that and look closely at the data and the graphs, you may discover the following:
1) At about 0.1 seconds there isn't much difference between the distance fallen or the velocity of the two balls. (This will be impossible to see in the graphs above; an inspection of the data is required.)
2) The time required for the golf ball to fall 10 meters (a reasonable distance for an experiment) is about 1.45s, while it takes the tennis ball about 1.48s to fall the same distance. The difference gets even greater the farther they fall: at 50 meters the golf ball takes about 3.43s while the tennis ball takes about 3.80s.
3) If, however, you drop the balls in a classroom from a height of only about 1 meter, the time difference will probably not be detectable by normal means. In fact, to fall 1 meter the golf ball takes 0.452s while the tennis ball takes 0.453s, a difference of only about a millisecond. Also according to the spreadsheet calculations the difference in distance between the two balls, at a nominal fall of 1 meter and at the same amount of time, is only about 4 millimeters (about 1/6 inch). You might be able to detect that difference if your observation skills are very good.

The terminal velocity of a golf ball, using either the calculators or the spreadsheet, is about 33.8 m/s, while that of the tennis ball is about 21.5 m/s. Clearly the golf ball falls "faster" than the tennis ball. There are two major reasons why this is so, in summary of all the above details:
1) The tennis ball is "fuzzy" and thus has a drag coefficient higher than that of the golf ball.
2) The density of the tennis ball is less than that of the golf ball.

John Link, MadSci Physicist