| MadSci Network: Physics |
That's a good question. It surely would be handy if the answer was "yes" ... but I'm afraid that it is not. In order to explain, I've made a figure.

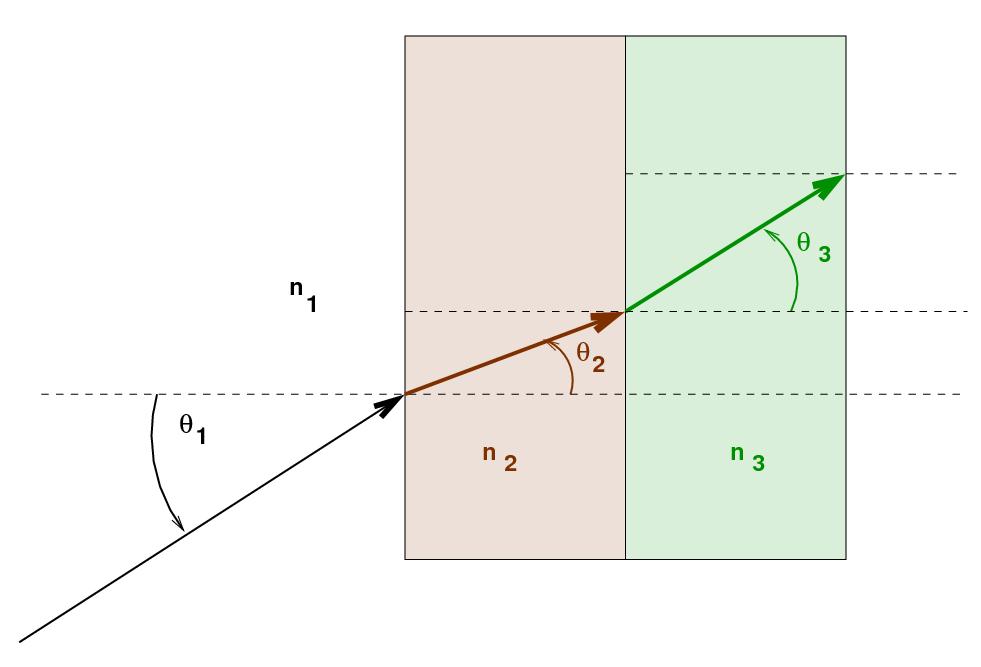
A ray of light travels through the air (medium 1, with index n1), from the lower-left to upper-right. It strikes an object which is made of two different types of glass: the first section has index of refraction n2, and the second half has a different index of refraction n3. What happens to the ray of light?
At the first interface, when the ray enters the brown glass with index n2, the ray refracts so that the angle theta2 is given by Snell's Law:
n2 * sin(theta2) = n1 * sin(theta1)
At the second interface, the ray moves from brown glass with index n2 to green glass with index n3. We can calculate the angle theta3 using Snell's Law again:
n3 * sin(theta3) = n2 * sin(theta2)
So, if we consider this entire object as a single chunk of glass, it takes a ray of light with initial angle theta1 and turns it into a ray with an angle theta3. We can solve for theta3 in terms of theta1 and the indices like so:
-1 [ n2 * sin(theta2) ]
theta3 = sin [ ------------------ ]
[ n3 ]
-1 [ n1 * sin(theta1) ]
= sin [ ------------------ ]
[ n3 ]
Now, if your idea was correct, then we could find the index of refraction of the combined glass like this: n = n2 + n3. In THAT case, Snell's Law would predict a final angle theta3 which was
-1 [ n1 * sin(theta1) ]
theta3 = sin [ ------------------ ]
[ n2 + n3 ]
I think you can see that these two expressions for the final direction of
the light ray are not the same. That means that your idea is not correct.
Too bad -- it would make some problems simpler!
Try the links in the MadSci Library for more information on Physics.