Re: Can you explain how elevation of mountains and other points are determined?

Thanks Mark ,

What a tricky question ... because there are many ways of determining the height of a mountain or other point. Techniques over the years have changed so much and in the last 20 years computer based techniques have really taken over.

Lets look at a simple way that we might use to determine an elevation.

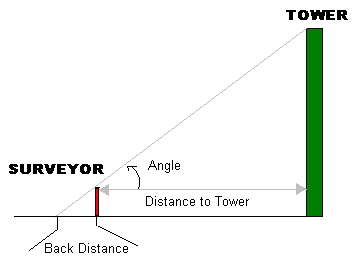
First we would measure the distance from ourselves to the 'mountain' Then using a device like a theodolite we measure the angle from our eye to the top of the mountain. Then we do a simple calculation using 'trigonometry' or 'geometry' to calculate the height.

You can try this for yourself : Have a look at my diagram . The calculations are below for your interest ... and you can try them out for yourself to measure the height of a building in your town. You can check your result by climbing the stairs to the roof and counting the steps ..

I have used meters but the results work out fine if you use feet or even paces. If you know the angle you can use trigonometry to get the height directly.

Tan ( angle ) = Height of tower / Distance to tower.

Hence: Height of tower = ( Tan ( angle ) * Distance to Tower ) + your height

Lets do an example:

Say you found that the distance from you to the tower is 120m and that you are 1.5m high and the angle is 45 degrees

Therefore:   Height of tower = ( Tan ( 45 ) * 120m ) + 1.5m 
             Height of tower = ( 1 * 120m ) + 1.5m 
             Height of tower = 121.5m 

Distance to tower / Back Distance = Height of Tower / Your height
Hence: Tower Height = [(Your height * Distance to tower)/back distance]+your height

Lets do another example using this method:

Say you found that the distance from you to the tower is 120m and that you are 1.5m high and the back distance is 1.5m too

Then : Tower Height = [ ( 1.5m * 120m ) / 1.5m ] + 1.5m 
       Tower Height = 121.5m 

Now back to the general subject.

In the past surveyors would use techniques like this and others, to determine the height of features in the landscape. Then using interpolation (guesswork) they could pass on to map makers (cartographers) the height of the area being mapped.

On a topographic map , the heights are recorded in 'spot heights' and in 'contour lines.' Contour lines join points of equal elevation above a specified reference.

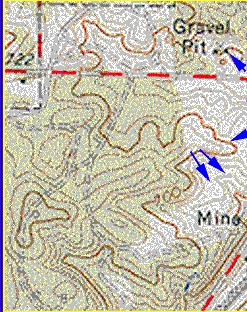Here is a part of a Topographic Map , Note the Brown Contour Lines.

Modern techniques have superseeded the tedious manual work of the surveyor/cartographer.

Today, heights can be determined using photogrammetry (heights are measured from photographs taken in an aeroplane), radar and general altimetry (height is determined directly using a baramoter or radar system), satellite observations (laser ranging), or with GPS (Global positioning systems) that can measure the position of a point on the surface very accurately using many satellites.

A GPS Satellite

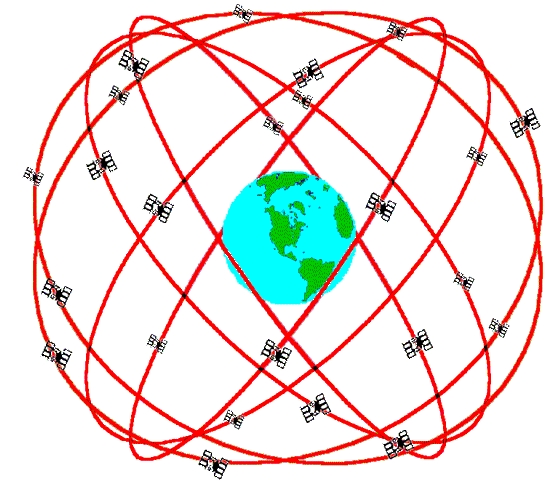
A GPS Constellation

GPS was designed by the military and is used in 'smart weapons' to make sure that missiles hit their targets acccurately.

What can we do with all of this height information:

Today the information is often used to create a computer model of the surface called a DTM (Digital Terrain Model) or DEM ( Digital Elevation Model) , these models can be used to create maps and some very exotic images of the surface.

A DTM of Mount St Helens Volcano:

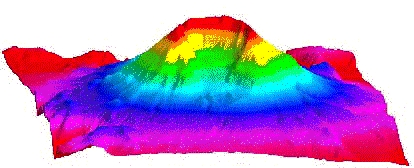
DTM's are used in

             Surveying and photogrammetry, 
             Civil engineering, 
             Planning and resource management, 
             Earth sciences, and 
             Military applications. 

It's a big subject, and here's a subtle point just to keep you thinking.

If the height of a mountain is measured as 'above sea level,' where is sea-level ???? There are entire organisations spending millions of dollars answering that question.

Here are some Keywords to try in your Internet search engine:

        GIS 
        DTM / DEM 
        GPS 
        Surveying 
        Cartography 
        Map Making 
        Topology 
        Topographic Map 
        Altimeter 
        Barometer 
        Plane Table Mapping 
        Radar Ranging 
        Photogrammetry 
        Air Photo Interpretation 
        Countour 
        Sea Level 
        Interpolation 

        National Center for Geographic Information 
        United States Geological Survey 
        TOPEX/Poseidon Satellite Project 

Geographical Information Systems: 
Principles and Applications, 
Longman Scientific & Technical, England.