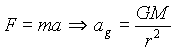
| MadSci Network: Physics |
My neighbor says that
the earth's escape velocity is a constant 11 km/s, regardless of the mass
of the body escaping, at least up to the point where the captive is equal
in mass to the captor. To prove his point he asks, assuming the moon was at
rest on the surface of the earth, "Is the mass of the moon significant to
change the velocity required for escape from the earths' gravity well to
<.05 or <.01?"
Since I believe the moon's gravity would increase the velocity necessary to
separate the two, my question is "Is the escape velocity for any two bodies
the sum of their separate escape velocities, computed assuming the escape
of an object with an insignificant gravitational force, i.e. in this case,
earth 11, moon 2 for a total of 13 km/s?
Though I am really rusty on my algebra, my guess is that an object 1/100th
the size of the earth or larger would increase the escape velocity by 1% or
more - Anything smaller than that would be insignificant.
Your neighbor is correct, but for the wrong reasons. The mass of the escaping body does not matter at all! The velocity required for any single body to "escape" the gravitational influence of any other body is dependent only on the mass of the second body, that is, the body being "left behind."
To understand why this is so, why escape velocity is dependent only on the mass of the body defined as being at rest, let's investigate how escape velocity is calculated.
In this discussion we will use the following conventions:
- A subscript letter g indicates something due to gravity.
- Upper-case M indicates the parent body, the one "being escaped from," which is defined as being at rest.
- Lower-case m indicates the subordinate body, the one "doing the escaping," which is in motion relative to the parent body.
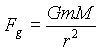 This is pretty well-understood and seems to be the source of your
difficulty. Newton's Third Law says that both masses (M and
m) will feel the same gravitational force. However, in order to produce motion
the force must act on a mass,
so that one of the masses (m) gets re-involved in the calculation.
This will ultimately lead to the counterintuitive conclusion that the value
of m doesn't effect the result!
This is pretty well-understood and seems to be the source of your
difficulty. Newton's Third Law says that both masses (M and
m) will feel the same gravitational force. However, in order to produce motion
the force must act on a mass,
so that one of the masses (m) gets re-involved in the calculation.
This will ultimately lead to the counterintuitive conclusion that the value
of m doesn't effect the result!
As an example, consider how we calculate the acceleration of any object in a gravitational field. Since force is mass times acceleration, we need to divide by the mass of the object (m) to get the acceleration. This leads us to the conclusion that the acceleration experienced by any object in the gravitational field of another object is independent of the mass of the subordinate object:
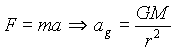
We see this in any situation involving orbiting objects for which the mass of one is a significant fraction of the mass of the other. Jupiter makes the Sun wobble considerably; their common center of mass (neglecting the other planets, which is a reasonable approximation since Jupiter contains 90+% of the total non-solar mass of the system) is about 2/3 of the way out from the center of the Sun.So far it looks good for your side -- see, this is a function of the substantial size of the second body! -- but perhaps we should keep going.
Now, since energy is defined as force times distance, and attractive forces are always defined as negative, the gravitational potential energy of any body in a gravitational field is given by
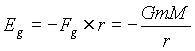
Now we know the expression for kinetic energy: ½mv2. Thus, if the "escape" kinetic energy equals the gravitational potential energy,
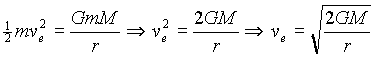
The only assumption here is that the inertial mass (involved in the expression for kinetic energy) is equal to the gravitational mass, or in other words, the m on the left side of the equation is equal to the m on the right side. This assertion has been tested many times and never found to be false.
Or, to answer your question more directly, it is not
true that
the escape velocity for
any two bodies the sum of their separate escape velocities.
| Dan Berger | |
| Bluffton College | |
| http://cs.bluffton.edu/~berger |
Try the links in the MadSci Library for more information on Physics.