Date: Thu Sep 16 02:45:50 1999
Posted By: Yaxun Liu, Grad student, Electrical Engineering, National University of Singapore
Area of science: Physics
ID: 936896916.Ph
Message:
These are very good questions which can help us understand
the interaction of electromagnetic field and matter.
First let's resolve the paradox of Faraday's disc.
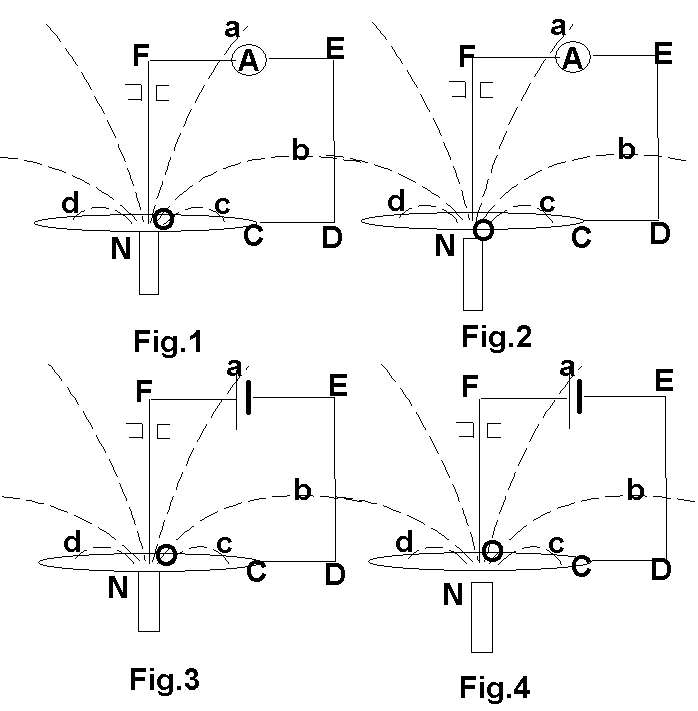 In fig.1 and
fig.2 the Faraday's disc serves as a generator. In fig.1 the magnet is
attached to the disc. When the disc is rotating, no electromotive force
(EMF) is generated across its radius (OC) since the disc has no relative
movement to the magnet. However, since the magnetic force line is moving
across the wire segments CDEFO, a EMF is generated along CDEFO and a net
EMF is resulted in the loop OCDEFO, which causes a current. In other words,
it is equivalent to fixing the disc and the magnet and rotating the wire
frame around them.
In fig.1 and
fig.2 the Faraday's disc serves as a generator. In fig.1 the magnet is
attached to the disc. When the disc is rotating, no electromotive force
(EMF) is generated across its radius (OC) since the disc has no relative
movement to the magnet. However, since the magnetic force line is moving
across the wire segments CDEFO, a EMF is generated along CDEFO and a net
EMF is resulted in the loop OCDEFO, which causes a current. In other words,
it is equivalent to fixing the disc and the magnet and rotating the wire
frame around them.
In fig.2 the magnet is detached from the disc. If the disc is rotating,
there is a EMF generated along OC but not along CDEFO, and therefore a
net EMF in the loop. However, if the disc is stationary but the magnet
is rotating, EMF's are generated along both OC and CDEFO, but they cancel
each other and there is no current in the loop.
In fig.3 and fig.4 the Faraday's disc serves as a motor. In fig.3 the
magnet is attached to the disc while in fig.4 it is detached from the disc.
In both cases there is a loop of current in OCDEFO therefore a torque on
the current. This torque tends to rotate both the disc and the wire frame
around the magnet. However, in fig.3 the disc is attached to the magnet
and the wire frame is constrained by supporting structures, therefore both
of them will not rotate. In fig.4 the wire frame is constrained by
supporting
structures but the disc can rotate, so it just rotates under the torque.
Now the question: Does the current in the disc (acting either as
generator
or motor) react against the mechanical magnet or against the magnetic
field?
Answer: Generally, the current reacts against electromagnetic fields.
The current is actually charged particles which are moving. Moving charged
particles generate electromagnetic fields and "feel" forces exerted by
electromagnetic fields. Charged particles interact with each other through
"disturbance" of electromagnetic fields, which propagates at the speed
of light. Electromagnetic fields have momentum and kinetic energy
distributed
over the whole space. When a moving charged particle changes its momentum
or kinetic energy by interaction with the electromagnetic fields, it causes
a disturbance of the momentum or kinetic energy distribution of the
electromagnetic
fields surrounding it, and this disturbance propagates through the space
and affects other charged particles.
Question: If against the magnetic field, how is this reaction force
"absorbed"? Does the answer to the above explain how attaching the magnet
to the rotating disc prevent motor action but not generator action?
To generate equal amounts of output power with and without the magnet
attached
to the disc, is equal mechanical input power required?
Answer: The "reaction force" exerted by a charged particle on the
electromagnetic
fields can be described by the exchanges of momentum and kinetic energy
between them, as explained in my answer to the previous question. This
does not explain how attaching the magnet to the rotating disc prevent
motor action but not generator action since in both cases the interaction
mechanism is the same. According to the energy conservation theorem (until
now, there is still absolutely no concrete evidence to overthrow it :-),
to generate equal amounts of output power with and without the magnet
attached
to the disc, equal mechanical input power is required, if the friction
between the magnet and the air can be ignored.
Question: Why do physics books always discuss the force on a charged
particle moving in a magnetic field, but never, that I have seen, the force
of a charged moving particle on the field? Is there a force on the
field (invoking Newton's laws dosen't "explain" a YES answer)
Answer: A charged moving particle does exert a "force" on the field,
however, this "force" can only be represented by the exchange of momentum
and energy between the particle and the electromagnetic fields, therefore,
its calculation is based on the definition of the momentum and energy of
the electromagnetic fields, which is complex. That may be the reason why
most physics books do not discuss the force of charged moving particle
on a field.
References
[1] L. Pearce Williams, Michael Faraday, A Biography, Reprint,
originally
published: New York: Basis Books, 1965, ISBN 0-306-80299-6, pp.194-197,
pp.202-204. This book has a brief description of the Faraday's disc.
[2] Marijan Ribaric, Luka Sustersic, Conservation Laws and Open
Questions
of Classical Electromagnetics, World Scientific Publishing, ISBN
981-02-0151-6
[3] http://www.amasci.com/free
nrg/n-mach.html.
This is an interesting article about the "homopolar generator" (actually
it's just Faraday's disc with attached magnet). It also gives some links
to related topics. There is a flood of materials about the "free-energy"
machine based on Faraday's disc on the web, but their credibility
is deeply doubted. From my personal point of view, there is no mystery
in the Faraday's disc which can not be explained by the classical physics.
Current Queue |
Current Queue for Physics |
Physics archives
Try the links in the MadSci Library for more information on Physics.
MadSci Home | Information |
Search |
Random Knowledge Generator |
MadSci Archives |
Mad Library | MAD Labs |
MAD FAQs |
Ask a ? |
Join Us! |
Help Support MadSci
MadSci Network,
webadmin@www.madsci.org
© 1995-1999. All rights reserved.
 In fig.1 and
fig.2 the Faraday's disc serves as a generator. In fig.1 the magnet is
attached to the disc. When the disc is rotating, no electromotive force
(EMF) is generated across its radius (OC) since the disc has no relative
movement to the magnet. However, since the magnetic force line is moving
across the wire segments CDEFO, a EMF is generated along CDEFO and a net
EMF is resulted in the loop OCDEFO, which causes a current. In other words,
it is equivalent to fixing the disc and the magnet and rotating the wire
frame around them.
In fig.1 and
fig.2 the Faraday's disc serves as a generator. In fig.1 the magnet is
attached to the disc. When the disc is rotating, no electromotive force
(EMF) is generated across its radius (OC) since the disc has no relative
movement to the magnet. However, since the magnetic force line is moving
across the wire segments CDEFO, a EMF is generated along CDEFO and a net
EMF is resulted in the loop OCDEFO, which causes a current. In other words,
it is equivalent to fixing the disc and the magnet and rotating the wire
frame around them.