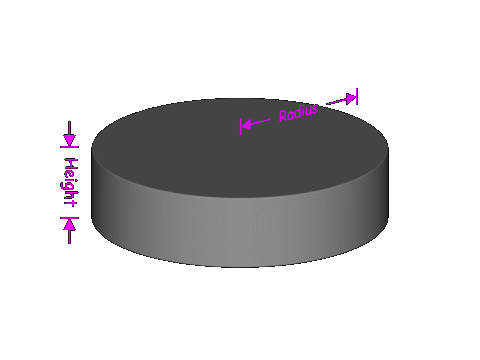
If we assume that the density in the disk is a constant (ρ), and that the disk has a uniform height (h), then the mass enclosed within radius r will be:
| MadSci Network: Astronomy |
Start with a simple model of a spiral disk as a cylinder:

If we assume that the density in the disk is a constant (ρ), and that
the disk has a uniform height (h), then the mass enclosed within radius r
will be:
M(r) = 4π *r2 * h * ρ
Since the radius does not come into the height part of the volume calculation at all, you will see that this gives a r2 dependence. This is a reasonable first-order approximation for the mass within radius r.
However, the density does vary in a spiral galaxy. In addition, we know that disks of spiral galaxies don't have the same thickness throughout. Thus to do the calculation properly for a given spiral you would need to know how the density varies with radius, and integrate:
M(r) = ∫ ρ(r) h(r) r dr
For example, we know that density for a spiral with a ring is not uniformly changing outward, and this would need to be taken into account.
For more detailed information (at the undergrad astro major level) on galactic astronomy and galaxies in general, I recommend Galactic Astronomy by Binney and Merrifield (or alternately the older version by Mihalas and Binney, but that is much harder to find).
Try the links in the MadSci Library for more information on Astronomy.