Re: Calculate max height of liquid (i.e. coke) in a cup with acceleration

Hi Carlos,

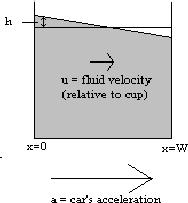
In answer to your question, sure! Let's start by thinking about a car, accelerating at rate a, and a cup of width W which is filled with, say, coke. We need two coordinates: x is in the direction the car is traveling, measured from the back of the cup, and h is the height of the liquid surface, measured from the top of the liquid as it lies flat. We'll also keep track of u, the speed of the fluid in the direction the car is traveling, measured relative to the cup:

We'll need three pieces of physics, probably the three most important ones in fluid dynamics: conservation of momentum, hydrostatics, and conservation of mass. I don't know your background so you may already know some of this.

Conservation of momentum

This is Newton's familiar law, "force equals mass times acceleration", or F = mu_t. I write u_t for acceleration to stress that acceleration of the fluid is the change in the fluid velocity u over time t. (Also, a is already taken, for the car.) For fluids, it's easiest to let F be the force per unit volume, and use the mass per unit volume, or density, d, to write F = du_t, or

u_t = F/d .

But there's a twist! Newton's laws don't take into account any accelerations of the reference frame relative to the fluid. But the car, passenger, and cup form a rigid system that is being accelerated "out from under" the fluid! The car is speeding up, but the fluid, if it could, would maintain a constant speed. From inside the car, we observe the fluid to be accelerated backward, at a rate opposite the car's acceleration. To take this into account, we write

u_t = F/d - a .

Hydrostatics

If the fluid surface is level, then two points at the same depth will have the same amount of water above them, and will be at the same pressure. But if the surface is tilted, then the point under more water will be under higher pressure. There will be a horizontal force from high pressure to low pressure.

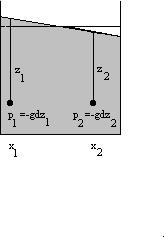
The strength of the pressure difference between points is p₂-p₁ = -gd(z₂-z₁) = -gd(h₂-h₁). If the pressure is higher on the left, there will be a force toward the right, and vice versa. The strength of the force depends on the surface tilt: if h changes a lot in a short space, then the pressure difference will be strong; if it is a gradual change, it will be weak. The total force between two points is the pressure difference between the points divided by the distance between them, F = gd(h₂-h₁)/(x₂-x₁) .

I'll use the notation h_x = (h₂-h₁)/(x₂- x₁) --in other words, h_x is the surface tilt. Then we can write F = gdh_x. Plugging this into the momentum conservation law gives

u_t = gh_x - a .

[Digression: a simpler problem]

Before taking up the third piece, volume conservation, we can use what we have so far to learn something about the system by asking a simpler question: if the car's acceleration a is constant, what does does the fluid look like in equilibrium--that is, when it is not moving and all the forces are in balance? In some ways this question doesn't make sense, since a car can't keep accelerating at the same rate indefinitely. But we only need it to accelerate at a constant rate long enough for the fluid to "settle down" to a final state.

If the fluid is not moving then its velocity is not changing and u_t = 0. This immediately gives h_x=a/g. Since g is negative (and assuming a is positive), the tilt is downwards, like in the two diagrams above. Using the definition of h_x and the fact that the total volume of fluid doesn't change, you can figure out that the height of the fluid on the back of the cup is -aW/2g. (If the cup had sloping sides, this same calculation would become a bit of a geometry puzzle!)

The main point is that in equilibrium, the forward pressure due to the tilted surface balances the tendency of the fluid to stay behind as the car accelerates forward. Note that the density of the fluid has dropped out of the problem. A denser fluid will have a stronger tendency to lag behind as the car accelerates, but a denser fluid will also have a greater pressure difference for the same surface tilt. The two effects cancel.

But that's not what you asked. The challenge of your question is the word "suddenly": we can no longer consider a fluid which is already tilted just right to balance the acceration; it has to start out flat. To proceed, we need to think about how the surface tilt changes, and for that, we need ...

Conservation of mass

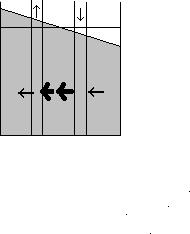
This is quantified by the relationship

u_x = -h_t,

that is, in any narrow region of the cup, the change in u over x is related to the change in h with time. You can explore this statement by picking values for the width and height of a region and of the velocities in and out, and calculating the change in volume of the slice in, say, a second. How much does the surface have to rise in that second to compensate? (Warning: this ignores differences in the heights of the two edges of the region due to the surface tilt. As long as the surface displacement is small compared to the total depth of the fluid, this is a good approximation.)

Putting it together

We can now try and answer your question. What do we know? We know how surface tilt is related to the car's acceleration and to the fluid's acceleration,

u_t = gh_x - a ,

and we know how surface height is related to the fluid velocity,

u_x = - h_t.

We also know that u = 0 at the two walls of the cup, and that h = 0 (the surface is level) at time t = 0. That's enough information to determine the height of the fluid surface in the cup at any point x at any time after the acceleration starts. (Actually, it's not quite enough information. You also need information about how to solve problems like these! The text by Haberman is a good one.)

The answer is

h(x,t)=(a/g)(x-W/2)+[4aW/(g*pi)]*[h₁ + h₃ + h₅ + ... ]

where pi = 3.141... and h_n= (1/n²) cos(n*pi*x/W) cos(sqrt(-g)*n*pi*t/W) . The more h_n's you add in, the more accurate the answer is, but each higher h_n adds a smaller and smaller correction. In practice, the first three do a pretty good job, and you'll barely notice the corrections if you go higher than about h₉.

If you study this you'll see that, as expected, the fluid gets highest at x = 0, the back wall of the cup. I plotted h at x = 0 for a = 5 mph per second, and for a cup of W = 8 cm (a pretty wide mug):

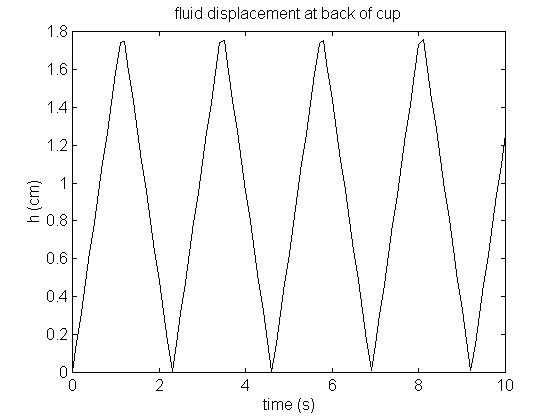
Looking at similar plots for different places in the cup shows that the surface oscillates between lying flat and a maximum tilt, which is approximately twice the equilibrium tilt we calculated above:

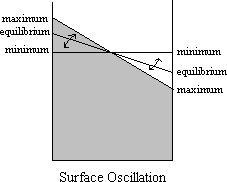
The maximum height is slightly larger than (aW/g)(4/pi² - 1/2), or approximately 0.01aW.

Math vs. reality

1. On the graph, you'll see that it takes over a second for the fluid to first reach its full height. This is due to the wide cup-- inspecting the solution will show you that the speed at which the fluid climbs depends only on W and gravity.
2. Real fluids have some friction. Not much, but enough to gradually wind the oscillations down until the fluid settles at the equilibrium position. However, some fluids have a lot of friction, which would make these equations wrong: they won't work for a milkshake!
3. Real cars don't accelerate at a constant rate for more than a few seconds at a time. Having a change with time complicates the math quite a bit. But as a model for when the car first starts, which is where our question was focused, this isn't bad.
4. Most cups are round, so W takes on several different values. I haven't verified this rigorously, but based on my experience with coke and cars I'm pretty sure there is not much flow perpendicular to the direction the car is moving. To get the height of the fluid somewhere other than the very back of the mug, just change W.
5. Many cups have sloping sides. This complicates the math a bit, but if the change in width of the cup is small compared to its total width it shouldn't alter the overall answer too much.

Drive carefully!

Dan Goldner (goldner@mit.edu)
MIT/Woods Hole Joint Program in Oceanography

Reference