Re: Distance liquid will travel through a given space.

Dear Tim,

First, let me apologize for the long delay in answering ... I am in the midst of a busy time at my job right now.

This is pretty much a simple first-year engineering problem ... unfortunately I got rid of all those books! But I think I got the correct solution.

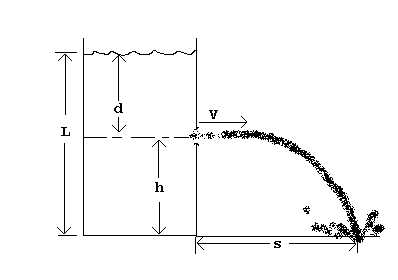
First, a diagram of the problem:

There are two applicable equations:

1) Flow of liquids from tank openings: consider a jet whose velocity is "V" discharging from an open tank through an opening on the side of the tank. The liquid depth *above* the opening is "d".  The velocity of the jet (ideally) is V=sqrt[2gd]  (where "g" is the acceleration of gravity). The actual velocity of the jet will be slightly less than the ideal velocity, depending upon the exact shape of the hole -- for example, a short tube instead of a smooth hole will reduce the jet velocity to about 80% of the ideal velocity. But for our purposes, we will use the maximum possible velocity, V=sqrt[2gd] .

2) Distance covered by a projectile under gravity: our "projectile" is a bit of liquid with a given starting velocity. Assuming that the jet is coming out of straight out of the side of the tank, it initially only has an ' x ' component of motion, so Vx = V.  It immediately starts to fall towards the ground. The time required to fall to the ground is t=sqrt[2*h/g] (where 'h' is the height of the hole above the ground). The x-distance "S" covered during that time = V * t = V * sqrt [2 * h/g]

If we put eqn 1 into eqn 2 for "V", we reduce to : S = sqrt [ 2gd * 2h/g ] = 2 sqrt [d * h]

If you prefer, you could express this as a function of the total liquid level "L" (given that d= L - h) as :

S= 2 sqrt [ L * h - h^2 ]

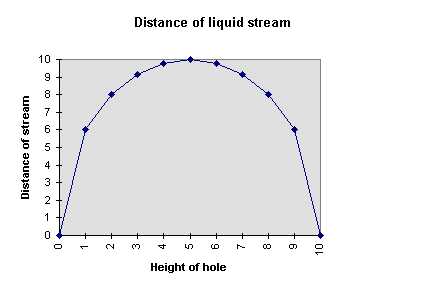
I plotted this equation, given "L" = 10, and plotting the distance of the stream as a function of the height of the hole "h". The result is a sort of parabolic, with the maximum distance obtained when the hole is halfway up the tank! (h = L/2) Maybe just what one would have guessed ... but I didn't guess that, so it was a little surprising to me to be so simple. Note that the maximum distance is equal to the total liquid height.

[One can also, more properly, find the maxima of the equation by differentiating to get : dS/dh = 2(L - 2 h)/sqrt(Lh - h²); setting equal to 0 to find the maxima, and solving for h you get h= L/2. Plugging that into the equation, S (at h=L/2) = L. .... But it's easier just to look at the graph, eh?]

It's always good to look at results like this to make sure they make sense, and they seem to in this case. If the hole is close to the top of the tank, then it doesn't go very far because the velocity is low (since there is little liquid pressure forcing it out); on the other hand if the hole is close to the bottom of the tank, there will be a lot of liquid pressure creating a high-velocity stream, but since it is close to the ground, it won't go very far away from the tank before hitting the ground. (It will still make a mess of liquid on the ground, though, and do it faster than a hole at the top!)

Regards,

Tod