Re: How does angle of plates effect force between two charged plates?

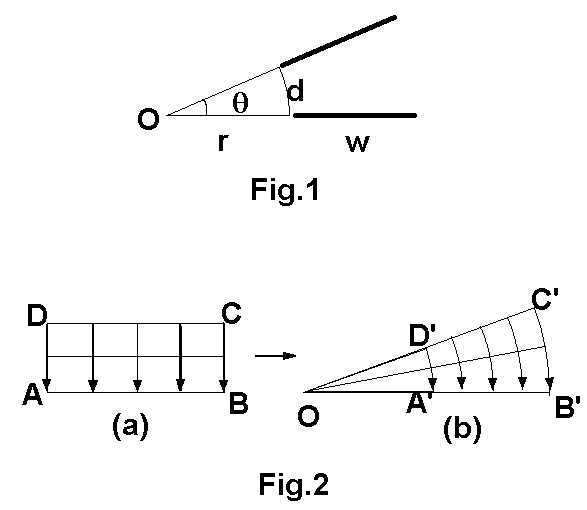If the required accuracy is not high, an approximate formula may be 
used. Assume the two plates are arranged as in figure 1, the angle 
between the two plates is theta, their nearest distance is d, the
width of the plates is w. Then the distance between their nearest 
ends to their axis is 

r = d/2/sin(theta/2)

The shape of the field line and potential lines for the angled
plates can be obtained through conformal mapping, as shown in
fig.2.
It is obvious that the electric field is not evenly distributed.
Denote the electric field at a point whose distance from O is
rho as E(rho), 

E(rho)=V/(rho*theta)

Then the surface charge density is

sigma(rho)=epsilon0*E(rho)

The total charge on one plate is obtained by integrate sigma(rho)*L
with rho from r to r+w, which results in

Q=epsilon0*V/theta*ln(1+w/r)*L

where L is the length of the plate.

Therefore the capacitance is

C=Q/V=epsilon0*ln(1+w/r)*L/theta

With these equations, we can then calculate the electric field
when either the charge or the voltage is known.

These equations ommit the fringing effects both in the directions of 
length and width. They are applicable only when the width and length
of the plates are much larger than the distance between them.

There is no simple closed-form expression for the relationship between
the angle and the force produced between the two plates. Numerical
methods must be used for the calculation of the electric field. You
can use either conformal mapping or method of moments for such
calculations.

The idea of using conformal mapping to solve for the electric field
is like this. If we assume the length of the plate is large enough
that the electric field between most part of the two plates behaves
like between two infinitely long plates, we can simplify the problem
as a 2-D problem. The potential satisfies the Laplace equation and
the boundary conditions at the two plates. The good point is, if
we have a set of simple boundary conditions and a solution (represented
by the potential lines and field lines) to the Laplace equation.
After a conformal mapping, the transformed solution is still
the solution of the Laplace equation, and it satisfies the transformed
boundary conditions. Therefore our task now is to find a simple
boundary condition and a conformal mapping which can transform
the simple boundary into the boundary in our problem. It is not
always easy to do so, and numerical calculations are generally needed.

There is a matlab package for conformal mapping 

(http://amath.colorado.edu/appm/faculty/tad/research/sc.html)
.
You can also find some useful links about conformal mapping on 
this page.

As to the method of moments, the idea is quite simple. Instead of
solving for the electric field directly, we try to solve for the
charge distribution on the plates. If we know the charge distribution,
we can easily calculate the field through Coulomb's Law.

(http://www.trea sure-troves.com/physics/physics.html)

How do we calculate the charge density on the plates? Well, we divide
each plate into small rectangles and we assume each rectangle has
evenly distributed surface charge. Suppose we have totally N rectangles,
then we have N unknowns, sigma(1), sigma(2)... sigma(N), which denotes
the surface charge density on each rectangle.

Now we need some equations for solving for sigma(n), n=1,...,N. We
use the boundary condition on the metal surface, that is, the tangential
component of the electric field should be zero. Since we have N unknowns,
we need N equations. We set up the equation at the center of each
rectangle, and we denote the tangential electric field at the center
of the m-th rectangle as E(m), now we have N equations: 

E(m)=0, m=1,...,N.

Now we need to represent E(m) in terms of sigma(n). It's simple, just
use the Coulomb's Law and integrate over each rectangle. Since the 
electric field is linear to the charge, we can extract sigma(n) out
of the integration and the integration can be carried out numericaly.
Finally we obtain a set of linear equations like these:

Z(m,1)*sigma(1)+Z(m,2)*sigma(2)+...+Z(m,n)*sigma(n)=0, for m=1,...,N.

Actually it is just a matrix equation

[Z][sigma]=0

The equation is not unique. If we have a solution and we multiply it
by a factor, the result is still a solution. But this kind of difference
is trivial to us. The simplest method to get some solutions in numbers
is to let one unkown to be 1 and solve for others.

The above is an over-simplified description of the method of moments.
There are some practical issues in its implementation, mainly about
the singularity handling when the observation point is in the source
area, but it's not very difficult and the work-around can be found
in the following references:

R. F. Harrington, Field Computation by Moment Methods. New York: 
Macmillan, 1968.

S. M. Rao, D. R. Wilton, and A. W. Glisson, "Electromagnetic scattering 
by surfaces of arbitrary shape," IEEE Transactions on Antenna and 
Propagation, AP-30, 407-418, May 1982. 

D.R.Wilton, S.M.Rao, A.W.Glisson, D.H.Schaubert, O.M.Al-Bundak, and 
C.M.Butler, "Potential integrals for uniform and linear source distribution 
on polygonal and polyhedral domains," IEEE Trans. Antennas Propagat., 
vol.AP-32, pp.276-281, Mar. 1984