Re: What does an observer see inside a spherical mirror?

It's simply a matter of considering the inside surface of the sphere as a concave mirror. Please read through the entire Lesson 3 of the page referenced in this URL.

There is a major constraint in the problem that you propose: Neither the observor nor the object can be farther than 2R from the central reflection point (Point "A" in the drawing of the referenced URL.), for a sphere of radius R, because both are inside the sphere! Let's divide the problem into three areas:
1) The object is in the space between d_o = "almost zero" and d_o = f.
2) The object is in the space between d_o = f and d_o = R.
3) The object is in the space between d_o = R and d_o = 2R.
We will use the "mirror equation" found here.

Case 1: If d_o = "almost zero" then d_i = negative "almost zero". If d_o = 1.0 (= f) then d_i = negative infinity, which means that the rays of light are collimated. Between these two limits the image distance is negative, meaning that it is a virtual image outside the sphere (to the right of the right surface), and our eye sees an upright virtual image, "behind" the surface of the mirror (outside the sphere). The perceived size of the image goes from the same size as the object to HUGE.

Case 2: If d_o = f then d_i = positive infinity, which means that the rays of light are collimated. If d_o = R (the object is at the center of the sphere) then d_i = R. The image, except for where d_o = f, is an inverted (upsidedown) real image, and our eye can focus the image if our eye is sufficiently far away from the image. "Sufficiently far" depends on each person's eyes, with normal young eyes being able to be accommodate (focus) for smaller distances than normal old eyes (which have lenses that practically do not focus).

Case 3: If d_o = R then d_i = R. If d_o = 2R then d_i = 4/3. The image is inverted (upsidedown) and real, and our eye can focus the image if our eye is sufficiently far away from the image. "Sufficiently far" depends on each person's eyes, with normal young eyes being able to be accommodate (focus) for smaller distances than normal old eyes (which have lenses that practically do not focus).

Applying the "mirror equation" to an Excel spreadsheet produces the following graph:

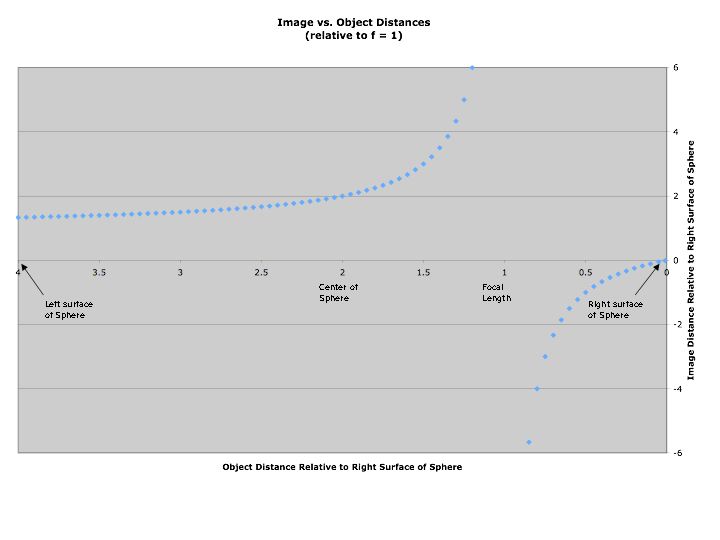
Notice several things, which have already been mentioned, at least in part, above:
1) As mentioned above, as the object distance gets close to the focal length the image distance approaches negative infinity. Because the image is virtual it can be "farther away" than the physical surface of the sphere.
2) When the object distance is greater than the focal length the image distance decreases from positive infinity down to 1.333. But the image distance is limited by the surface of the sphere, so d_i can not be any greater than 4.0 without reflecting again from the mirror. See part 3) below. The limit of 1.333 is because the object can not be outside the sphere and so d_o is limited to 4.0.
3) With the object distance between 1.0 (f) and 1.333, the image distance is greater than the opposite surface of the sphere (d_i > 4). In that case we can calculate the secondary image. For instance, if the object is at 1.25 then the image distance is 5.0; this puts the image at -1.0 with respect to the left surface, meaning that the secondary "object" has a distance of -1.0. Putting that into the equation gives us d_i = 0.5, so the final image is observable if we could turn around and look the other way without our head getting in the way!

You can work with the equation to work out other situations. Have fun!

John Link, MadSci Physicist