| MadSci Network: Physics |
The question: Area of light beam against 45 degree incline? I'm trying to find out the area a horizontal, circular beam of light will make on a 45 degree incline. If the beam makes a circle with a 1 inch diameter against a vertical wall at a distance of 1 foot, what would be the area of the light beam if the wall was pivoted 45 degrees away from the beam, at the point of light contact?
The question has a possibly simple answer, and a possibly more difficult answer. The simple answer, which depends on the beam's being fairly constant in its cross section (which would mean that the beam from the source is well collimated and cylindrical in shape), is that the shape of the beam on a 45-degree surface would be an ellipse having a major axis of 1.414 inches and a minor axis of 1.000 inches. This is because a slice through a cylinder obtains an ellipse with major axis of length d/cos(theta) where theta is the tilt angle and d is the diameter of the cylinder. Now, the area of an ellipse is PI*a*b where "a" is the semimajor axis (also called the major radius) and "b" is the semiminor axis (also called the minor radius) of the ellipse (see Area of Ellipse at Wikipedia) (If the ellipse is a circle then a = b = r and we have the familiar equation Area = PI*r2.), so the area of the ellipse having 2a = 1.414 inches and 2b = 1.000 inches is PI*(1.414/2)*(1.000/2) = 1.111 in2, compared to a circle of diameter 1.000 inch having an area of 0.785 in2. In general, the area of the ellipse is 1/cos(theta) times the area of the circle, and this holds for the present example since 1.111/0.785 = 1.414.
The answer is more complicated if the beam is either converging or diverging. Please examine the following web sites:
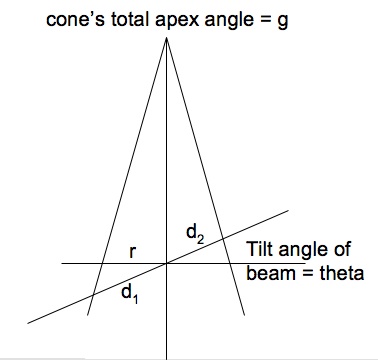
If the beam of light is either diverging (getting larger as it gets farther from the source) or converging (getting smaller as it gets farther from the source) it can be modeled according to the drawing below.

Unfortunately none of the usual "conic section" sites provides exactly what I'm looking for, so I have to do some derivation, although a good book on solid geometry might have the results (or something very similar). The drawing above is a cross section through the conical beam, the cone's apex angle being "g". (If it is a diverging beam the beam is shining from top to bottom, but if it is a converging beam it is shining from bottom to top. In either case the illuminated surface is represented untilted by the line that crosses perpendicularly to the cone's central axis, and by the tilted beam by the line with labels "d1" and "d2".) The tilt of the beam with respect to the surface is the angle theta, as before. If the beam were not tilted with respect to the surface the spot would be a circle of radius "r". With the tilt, the ellipse has its major axis (2*a) made up of the distances d1 and d2.
Without offering proof of the following (It is extremely detailed!),
here are the pertinent equations needed (angles are in degrees):
d1 = r sin(90 + g/2) / sin(90 - g/2 - theta)
d2 = r sin(90 - g/2) / sin(90 + g/2 - theta)
The needed dimensions of the ellipse are then
a = (d1 + d2) / 2
b = r / sin(phi)
where
phi = 90 - beta
and
beta = tan-1(o/r)
and
o = d1 - a
The distance "o" is an offset of the center of the ellipse from where
the central axis of the cone cuts through the ellipse, and is due to the
fact that d1 > d2.
The sum of the cone's apex half angle (g/2) and theta must be less than 90 degrees. With a and b you can figure the area of the ellipse, with the information given towards the top of this answer. I have made some calculations with various cone apex angles, with the tilt angle of the beam to the surface being 45 degrees, as before, but for simplicity I have used r = 1.00:
| Tilt angle = 45 degrees; r = 1 | ||||
| area of ellipse | ||||
| apex angle, degrees | d1 | d2 | o | / area of circle |
| 0 | 1.414 | 1.414 | 0 | 1.414 |
| 5 | 1.479 | 1.356 | 0.062 | 1.420 |
| 10 | 1.550 | 1.300 | 0.125 | 1.436 |
| 20 | 1.717 | 1.202 | 0.257 | 1.507 |
| 30 | 1.932 | 1.115 | 0.408 | 1.646 |
| 40 | 2.224 | 1.037 | 0.593 | 1.896 |
| 60 | 3.346 | 0.897 | 1.225 | 3.354 |
| 80 | 8.789 | 0.769 | 4.010 | 19.75 |
You can see that with the cone's apex angle being zero degrees, which is the same as a cylinder, the calculation indeed gives the proper ratio of the area of the ellipse to the area of the circle (1.414). As the cone's beam angle gets larger the area of the ellipse to that of the circle has a higher ratio.
John Link, MadSci Physicist
Try the links in the MadSci Library for more information on Physics.