Re: Formula to calculate the effort to pull a weight on wheels up an incline?

Hi Fred.

I'm a trailer sailor myself, so I'm pretty familiar with this problem.

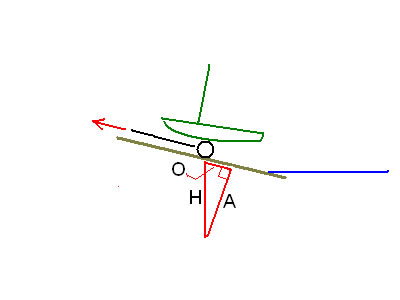
The illustration shows a single axle trailer sitting on a boat ramp. The triangle gives the relationship between the weight (hypotenuse) and the pull on the tongue (the opposite side of the triangle). The acute angle of the force triangle is the same as the angle of the ramp.

Let's say that the ramp has a slope of ten meters horizontally for every meter of vertical rise, and the boat, trailer and gear weigh (say) 5000 Newtons. The angle of the boat ramp is the inverse tangent of the rise divided by the run, or tan^-1[1/10], or about 5.71 degrees. The pull on the trailer tongue will be the boat's weight times the sine of that angle, or sine(5.71) X 5000 Newtons, or about 500 N.

Rolling friction of the tires is simpler. According to the Wikipedia article, http://en.wikipedia.org/wiki/Rolling_resistance the coefficient of friction of (rolling) rubber tires on concrete pavement is 0.010 to 0.015. The force required to overcome rolling resistance is the weight times the coefficient, or conservatively 5000 N X 0.015 = 75 N. Tire diameter doesn't have anything to do with it, although larger diameter tires will go over bumps easier. Bearing friction will be neglible at slow speeds.

There are so many other variables, and the speeds are so slow, that other sources of friction can be discounted.

If you are designing "tire stops, pulleys, winches or motorized assists" , you will probably want to multiply the force you calculate by a factor of two or three as a Factor of Uncertanity. Always take great care when maneuvering something as heavy and ungainly as a boat on a ramp.

Fair Winds!

C.H. "Chas" Hague, PE SE, United States Coast Guard Auxiliary