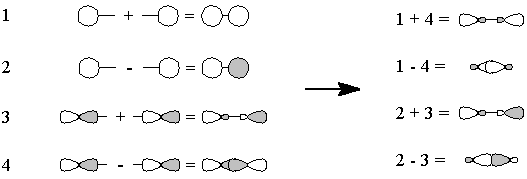1. Carbon monoxide in terms of hybridization and resonance (i.e. valence bond) theory.
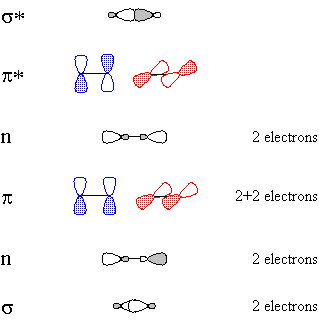
CºO, being linear, is described by hybridization theory as having sp-hybridized atoms. Carbon begins with one electron in each of the following orbitals: sp1, sp2, px, py, shown schematically in Figure 1.Oxygen begins with six valence electrons, distributed (for example) thus: one in sp1, two in sp2, two in px, one in py, shown schematically in Figure 2.
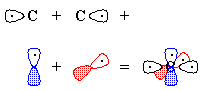 |
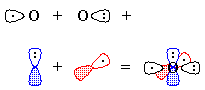 |
|
| Figure 1 | Figure 2 |
However, the one-electron orbitals on oxygen and carbon don't match up well, so we can fix things one of two ways:
- We "move" (this is pure bookkeeping!) an electron
from oxygen's px to carbon's
sp1, so that both atoms now have
the same electron configuration and can form a triple bond by the overlap
of the one-electron orbitals (Figure 3). There is one lone pair each on
carbon and on oxygen, and because we have "removed" an electron
from oxygen and "given" it to carbon, there are formal charges.
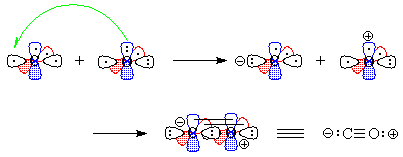
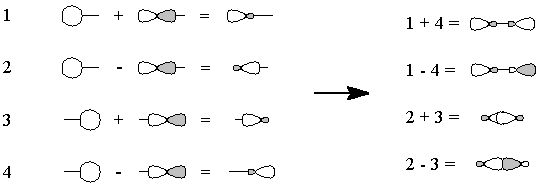
Figure 3 - We "move" an electron from px on carbon to carbon's sp1. Overlap of the remaining one-electron
orbitals results in a double bond, with one lone pair of electrons on
carbon and two on oxygen; all this is shown schematically in Figure 4.
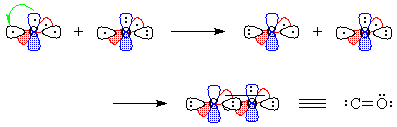
Figure 4
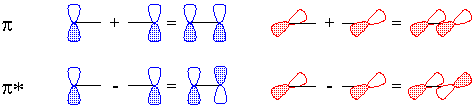
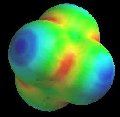
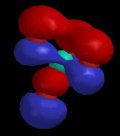
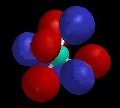
Of course, valence-bond theory requires that we mix these two models (which can in fact be stated mathematically); this is called "resonance" and is represented schematically in Figure 5. The true structure is neither of these models, but a combination, and includes contributions from electronegativity which shift electron density from carbon back to oxygen. The calculated charge density surface (HF/6-31G*) is shown in Figure 6.
 |
||
| Figure 5 | Figure 6 |